Абсолютная пропускная способность
Абсолютная пропускная способность – среднее число заявок, которое может быть обслужено в единицу времени. Характеризует интенсивность выходящего потока обслуженных заявок.| Тип СМО | СМО с отказами | СМО с очередью | СМО с неограниченной очередью |
| Одноканальные СМО | A = Q × λ = p0 × λ | A = Q × λ | A = λ |
| Многоканальные СМО | A = Q × λ | A = Q × λ | A = λ |
Исчисляем показатели обслуживания многоканальной СМО:
1. Интенсивность нагрузки.
Интенсивность нагрузки ρ=3 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания.
2. Время обслуживания.
3. Вероятность, что канал свободен (доля времени простоя каналов).
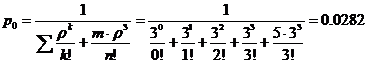
Вероятность того, что обслуживанием:
занят 1 канал:
p1 = ρ1/1! p0 = 31/1!·0.0282 = 0.0845
заняты 2 канала:
p2 = ρ2/2! p0 = 32/2!·0.0282 = 0.13
заняты 3 канала:
p3 = ρ3/3! p0 = 33/3!·0.0282 = 0.13
4. Доля заявок, получивших отказ.
Значит, 13% из числа поступивших заявок не принимаются к обслуживанию.
5. Вероятность обслуживания поступающих заявок.
В системах с отказами события отказа и обслуживания составляют полную группу событий, поэтому:
pотк + pобс = 1
Относительная пропускная способность: Q = pобс.
pобс = 1 - pотк = 1 - 0.13 = 0.87
Следовательно, 87% из числа поступивших заявок будут обслужены. Приемлемый уровень обслуживания должен быть выше 90%.
6. Среднее число каналов, занятых обслуживанием.
nз = ρ·pобс = 3·0.87 = 2.6 каналов
Среднее число простаивающих каналов.
nпр = n - nз = 3 - 2.6 = 0.4 каналов
7. Коэффициент занятости каналов обслуживанием.
Следовательно, система на 90% занята обслуживанием.
8. Абсолютная пропускная способность для многоканальной СМО.
A = pобс·λ = 0.87·6 = 5.2 заявок/мин.
9. Среднее время простоя СМО.
tпр = pотк ∙ tобс = 0.13∙ 0.5 = 0.06 мин.
10. Среднее число заявок, находящихся в очереди.
![]()
![]() ед.
ед.
11. Среднее время простоя СМО (среднее время ожидания обслуживания заявки в очереди).
![]() мин.
мин.
12. Среднее число обслуживаемых заявок.
Lобс = ρ·Q = 3·0.87 = 2.62 ед.
13. Среднее число заявок в системе.
LCMO = Lоч + Lобс = 1.9 + 2.62 = 4.52 ед.
13. Среднее время пребывания заявки в СМО.
![]() мин.
мин.
Число заявок, получивших отказ в течение часа: λ·p1 = 0.78 заявок в мин.
Номинальная производительность СМО: 3 / 0.5 = 6 заявок в мин.
Фактическая производительность СМО: 5.2 / 6 = 87% от номинальной производительности.
Перейти к онлайн решению своей задачи
Пример №2. Универсам получает ранние овощи и зелень из теплиц пригородного совхоза. Машины с товаром прибывают в универсам в неопределенное время. В среднем прибывает λ автомашин в день. Подсобные помещения и оборудование для подготовки овощей к продаже позволяют обработать и хранить товар объемом не более m автомашин одновременно. В универсаме работают n фасовщиков, каждый из которых в среднем может обработать товар с одной машины в течение tобсл дня. Определить вероятность обслуживания приходящей автомашины Pобс. Какова должна быть емкость подсобных помещений m1, чтобы вероятность обслуживания была бы больше или равна заданной величине, т.е. Pобс.> P*обс.
λ = 3; tобс = 0,5; n = 2; m = 2, P*обс = 0,92.
Решение.
Исчисляем показатели обслуживания многоканальной СМО:
Переводим интенсивность потока заявок в часы: λ = 3/24 = 0.13
Интенсивность потока обслуживания:
μ = 1/12 = 0.0833
1. Интенсивность нагрузки.
ρ = λ·tобс = 0.13·12 = 1.56
Интенсивность нагрузки ρ=1.56 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания.
Поскольку 1.56<2, то процесс обслуживания будет стабилен.
3. Вероятность, что канал свободен (доля времени простоя каналов).
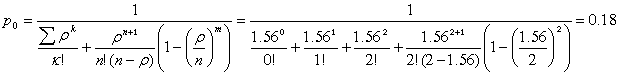
Вероятность того, что обслуживанием:
занят 1 канал:
p1 = ρ1/1! p0 = 1.561/1!·0.18 = 0.29
заняты 2 канала:
p2 = ρ2/2! p0 = 1.562/2!·0.18 = 0.22
4. Доля заявок, получивших отказ.
Значит, 14% из числа поступивших заявок не принимаются к обслуживанию.
5. Вероятность обслуживания поступающих заявок.
В системах с отказами события отказа и обслуживания составляют полную группу событий, поэтому:
pотк + pобс = 1
Относительная пропускная способность: Q = pобс.
pобс = 1 - pотк = 1 - 0.14 = 0.86
Следовательно, 86% из числа поступивших заявок будут обслужены. Приемлемый уровень обслуживания должен быть выше 90%.
6. Среднее число каналов, занятых обслуживанием.
nз = ρ·pобс = 1.56·0.86 = 1.35 канала.
Среднее число простаивающих каналов.
nпр = n - nз = 2 - 1.35 = 0.7 канала.
7. Коэффициент занятости каналов обслуживанием.
K3 = n3/n = 1.35/2 = 0.7
Следовательно, система на 70% занята обслуживанием.
8. Находим абсолютную пропускную способность.
A = pобс·λ = 0.86·0.13 = 0.11 заявок/час.
9. Среднее время простоя СМО.
tпр = pотк·tобс = 0.14·12 = 1.62 час.
Вероятность образования очереди.
10. Среднее число заявок, находящихся в очереди.
11. Среднее время простоя СМО (среднее время ожидания обслуживания заявки в очереди).
Tоч = Lоч/A = 0.44/0.11 = 3.96 час.
12. Среднее число обслуживаемых заявок.
Lобс = ρ·Q = 1.56·0.86 = 1.35 ед.
13. Среднее число заявок в системе.
LCMO = Lоч + Lобс = 0.44 + 1.35 = 1.79 ед.
13. Среднее время пребывания заявки в СМО.
TCMO = LCMO/A = 1.79/0.11 = 16.01 час.
Теперь ответим на вопрос: какова должна быть емкость подсобных помещений m1, чтобы вероятность обслуживания была бы больше или равна заданной величине, т.е. Pобс. > 0.92. Расчет производим исходя из условия:
![]()
где 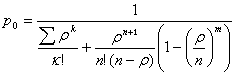
Для наших данных:
![]()
Далее необходимо подобрать такое k (см. п.3 "доля времени простоя каналов"), при котором pотк < 0.08 или pобс > 0.92.
например, при k = m1 = 4, pотк = 0.07 или pобс = 0.93.
Пример №3. На станцию технического обслуживания поступает простейший поток заявок с интенсивностью 1 автомобиль за 2 ч. Во дворе в очереди может находиться не более 3 машин. Среднее время ремонта - 2 часа. Дайте оценку работы СМО и разработайте рекомендации по улучшению обслуживания.
Решение:
Определяем тип СМО. Фраза « На станцию» говорит об единственном устройстве обслуживания, т.е. для проверки решения используем сервис Одноканальные СМО.
Определяем вид одноканальной СМО. Поскольку имеется упоминание об очереди, следовательно выбираем «Одноканальная СМО с ограниченной длиной очереди».
Параметр λ необходимо выразить в часах. Интенсивность заявок 1 автомобиль за 2 ч или 0,5 за 1 час.
Интенсивность потока обслуживания μ явно не задана. Здесь приводится время обслуживания tобс = 2 часа.
Исчисляем показатели обслуживания для одноканальной СМО:
Интенсивность потока обслуживания:
![]()
1. Интенсивность нагрузки.
ρ = λ·tобс = 0.5·2 = 1
Интенсивность нагрузки ρ=1 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания.
3. Вероятность, что канал свободен (доля времени простоя канала).
![]()
![]()
Следовательно, 20% в течение часа канал будет не занят, время простоя равно tпр = 12 мин.
4. Доля заявок, получивших отказ.
Заявки не получают отказ. Обслуживаются все поступившие заявки, pотк = 0.
5. Относительная пропускная способность.
Доля обслуживаемых заявок, поступающих в единицу времени:
Q = 1 - pотк = 1 - 0 = 1
Следовательно, 100% из числа поступивших заявок будут обслужены. Приемлемый уровень обслуживания должен быть выше 90%.
6. Абсолютная пропускная способность.
A = Q·λ = 1·0.5 = 0.5 заявок/час.
8. Среднее число заявок в очереди (средняя длина очереди).
![]()
![]() ед.
ед.
9. Среднее время простоя СМО (среднее время ожидания обслуживания заявки в очереди).
![]() час.
час.
10. Среднее число обслуживаемых заявок.
Lобс = ρ·Q = 1·1 = 1 ед.
12. Среднее число заявок в системе.
LCMO = Lоч + Lобс = 1.2 + 1 = 2.2 ед.
13. Среднее время пребывания заявки в СМО.
![]() час.
час.
Число заявок, получивших отказ в течение час: λ·p1 = 0 заявок в час.
Номинальная производительность СМО: 1 / 2 = 0.5 заявок в час.
Фактическая производительность СМО: 0.5 / 0.5 = 100% от номинальной производительности.
Вывод: станция загружена на 100%. При этом отказов не наблюдается.
