Поиск первоначального опорного плана
Предположим, что каноническая задача ЛП имеет не совсем специальный вид, а к примеру, правые части уравнений системы ограничений могут быть отрицательны.Этот случай возникает при решении задачи о рационе. Канонический вид задачи выглядит так:
-4x1-3x2-2x3+x4=-33
-3x1-2x2-x3+x5=-23
-x1-x2-2x3+x6=-12
xi≥0, i=1,6
F = 20х1 + 20х2 + 10х3 → min.
Запишем задачу в симплекс-таблицу (табл. 1).
Таблица 1
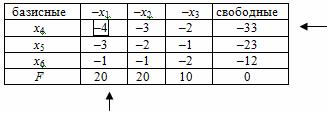
Базисное решение, соответствующее базису {x4, x5, x6} и равное (0; 0; 0; -33; 23; -12), не является допустимым ввиду отрицательности х4 < 0, x5 < 0, x6 < 0.
Сформулируем правило нахождения допустимого опорного плана.
Если в столбце свободных членов есть отрицательные элементы, выберите из них наибольший по модулю, а в его строке - любой отрицательный. Взяв этот элемент в качестве разрешающего пересчитайте таблицу по прежним правилам 2-5.
Если в полученной таблице все элементы столбца свободных членов стали положительны либо 0, то данное базисное решение можно взять в качестве первоначального опорного плана. Далее симплекс-методом дорешать задачу. Если в столбце свободных членов не все элементы неотрицательны, то еще раз воспользоваться этим правилом.
Проведем этот шаг для задачи о рационе. В качестве разрешающей строки табл. 1 нужно выбрать первую. А разрешающим элементом выберем, к примеру, элемент -4.
Таблица 2
| базисные | -х4 | -х2 | -х3 | свободные |
| х1 | 1/4 | 3/4 | ½ | 33/4 |
| х5 | -3/4 | 1/4 | ½ | 7/4 |
| ←х6 | -1/4 | -1/4 | -3/2 | -15/4 |
| ↑F | 5 | 5 | 0 | 165 |
Таблица 2
| базисные | -х4 | -х2 | -х6 | свободные |
| х1 | -1/3 | 2/3 | 1/3 | 7 |
| х5 | -5/6 | 1/6 | 1/3 | ½ |
| х3 | 1/6 | 1/6 | -2/3 | 5/2 |
| F | 5 | 5 | 0 | 165 |
F = 20х1 + 20х2 + 10х3 = 20 · 7 + 0 + 10·5/2 = 140 + 25 = 165.
В этой задаче не пришлось улучшать найденный первоначальный опорный план, т.к. он оказался оптимальным. Иначе, мы должны были вернуться к III этапу.
Решение задачи о плане симплекс-методом
Задача. Предприятие располагает тремя видами сырья и намеревается выпускать четыре вида продукции. Коэффициенты в таблице 3.12 указывают затраты соответствующего вида сырья на единицу определенного вида продукции, а также прибыль от реализации единицы продукции и общие запасы ресурсов. Задача: найти оптимальный план производства продукции, при котором будет обеспечена максимальная прибыль.Таблица 3
|
Виды продукции → Виды сырья ↓ |
I |
II |
III |
IV |
Запасы ресурсов |
|
1 |
5 |
0,4 |
2 |
0,5 |
400 |
|
2 |
0 |
5 |
1 |
1 |
300 |
|
3 |
1 |
0 |
1 |
1 |
100 |
|
Прибыль |
3 |
5 |
4 |
5 |
|
5x1+0.4x2+2x3+0.5x4≤400
5x2+x3+x4≤300
x1+x3+x4≤100
x1≥0, x2≥0, x3≥0, x4≥0
F = 3x1+5x2+ 4x3+ 5x4 → max.
Целевая функция выражает собой общую суммарную прибыль, полученную от реализации всей плановой продукции, а каждое из неравенств выражает затраты определенного вида продукции. Понятно, что затраты не должны превышать запасов сырья.
Приведем задачу к канонической форме и к специальному виду, введя дополнительные переменные х5, х6, х7 в каждое из неравенств.
Очевидно, что, если первого ресурса необходимо для производства плановой продукции 5х1 + 0,4х2 + 2х3 + 0,5х4, то х5 обозначает просто излишки первого ресурса как разность между имеющимся запасом и требуемым для производства. Аналогично х6 и х7. Итак, дополнительные перемены задачи ЛП обозначают излишки сырья, времени, других ресурсов, остающихся в производстве данного оптимального плана.
Запишем задачу в таблицу 4, предварительно выписав ее каноническую форму:
5x1+0.4x2+2x3+0.5x4+x5=400
5x2+x3+x4+x6=300
x1+x3+x4+x7=100
xi≥0, i=1,7
-F = -3x1-5x2-4x3-5x4 → min.
I этап. Это задача специального вида, базис составляют переменные {х5, х6, х7}, правые части уравнений неотрицательны, план х = (0, 0, 0, 0, 400, 300, 100) - опорный. Он соответствует симплекс-таблице.
Таблица 4
|
базисные |
-х1 |
-х2 |
-х3 |
-х4 |
свободные |
|
х5 |
5 |
0,4 |
2 |
0,5 |
400 |
|
х6 |
0 |
5 |
1 |
1 |
300 |
|
х7 |
1 |
0 |
1 |
1 ← |
100 |
|
-F |
-3 |
-5 |
-4 |
-5 ↑ |
0 |
II этап. Проверим план на оптимальность. Так как в индексной F-строке есть отрицательные элементы, то план неоптимален, переходим к III этапу.
III этап. Улучшение опорного плана. Выберем в качестве разрешающего столбца четвертый, но могли бы выбрать и второй, т.к. в обоих (-5). Остановившись на четвертом, выберем в качестве разрешающего элемента 1, т.к. именно на нем достигается минимум соотношений ![]() . С разрешающим элементом 1 проводим преобразование таблицы по правилам 2-5 (табл. 5).
. С разрешающим элементом 1 проводим преобразование таблицы по правилам 2-5 (табл. 5).
Таблица 5
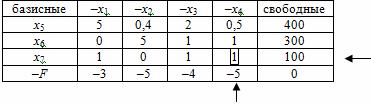
Полученный план опять неоптимален, т.к. в F-строке есть отрицательный элемент -5. этот столбец разрешающий.
В качестве разрешающего элемента выбираем 5, т.к. ![]() .
.
Пересчитываем еще раз таблицу. Заметим, что пересчет удобно начинать с индексной строки, т.к. если в ней все элементы неотрицательны, то план оптимален, и чтобы его выписать, достаточно пересчитать столбец свободных членов, нет необходимости вычислять "внутренность" таблицы (табл. 6).
Таблица 6
|
базисные |
-х1 |
-х6 |
-х3 |
-х7 |
свободные |
|
х5 |
|
|
|
|
334 |
|
х2 |
|
|
|
|
40 |
|
х4 |
|
|
|
|
100 |
|
-F |
1 |
1 |
1 |
4 |
700 |
IV этап. Базисные переменные {x5, x2, x4} принимают значения из столбца свободных членов, а свободные переменные равны 0. Итак, оптимальный план х* = (0, 40, 0, 100, 334, 0, 0) и F* = 700. Действительно, F = 3х1 + 4х3 + 5х2 + 5х4 = 5 · 40 + 5 · 100 = 700. Т. е. для получения максимальной прибыли в 700 руб. предприятие должно выпускать изделия II вида в количестве 40 штук, IV - вида в количестве 100 штук, изделия I и III вида производить невыгодно. При этом сырье второго и третьего вида будет израсходовано полностью, а сырья первого вида останется 334 единицы (х5 = 334, х6 = 0, х7 = 0).
