Задача составления кормовой смеси или задача о диете
Содержание- Задача о составлении рациона (задача о диете)
- Задача о смесях (смешивания этих ингредиентов в пропорциях)
- Задача об оптимальном составе бетонной смеси
Для того, чтобы цыплята достигли к 8-й неделе необходимого веса, кормовой рацион должен удовлетворять определённым требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов, или ингредиентов.
В таблице приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента. Смесь должна содержать:
- не менее 0.8% кальция (от общего веса смеси)
- не менее 22% белка (от общего веса смеси)
- не более 5% клетчатки (от общего веса смеси )
| Ингредиент | Содержание питательных веществ (кг/ингредиента) | Стоимость (руб./кг) | ||
| Кальций | Белок | Клетчатка | ||
| Известняк Зерно Соевые бобы |
0.38 0.001 0.002 |
- 0.09 0.5 |
- 0.02 0.08 |
0.04 0.15 0.40 |
Математическая формулировка задачи. Введём следующие обозначения:
X 1 - содержание известняка в смеси (кг);
Х2 - содержание зерна в смеси (кг);
Х3 - содержание соевых бобов в смеси (кг);
Общий вес смеси, еженедельно расходуемый на кормление цыплят: 20 000 х 0.5 = 10 000 кг.
Ограничения, связанные с содержанием кальция, белка и клетчатки в кормовом рационе, имеют вид:
0.38X1 + 0.001Х2 + 0.002Х3 ≥ 0.008 х 10 000,
0.09Х2 + 0.50Х3 ≥ 0.22 х 10 000,
0.02Х2+ 0.08Х3 ≤ 0.05 х 10 000.
Окончательный вид математической формулировки задачи:
min f(X) = 0.04 x1 + 0.15Х2 +0,40Х3
при ограничениях
Х1+Х2+Х3= 10 000
0.38Х1 + 0.001Х2 + 0.002Х3 ≥ 80
0.09Х2+ 0.50Х3 ≥ 2200
0.02Х2+ 0.08Х3 ≤ 500
Xj > 0, j = 1, 2, 3.
Перейти к решению симплекс-методом
Задача о составлении рациона (задача о диете, задача о смесях)
Пример №1. Имеется два вида продукции П1 и П2, содержащие питательные вещества S1, S2, S3, S4 (жиры, белки, углеводы, витамины). Содержание числа единиц питательных веществ в единице каждого вида продукции и необходимый минимум питательных веществ приведены в табл. 2.Таблица 2
Питательные вещества | Число единиц питательных веществ в единице продукции | Необходимый минимум питательных веществ | |
| П1 | П2 | ||
| S1 | 1 | 2 | 10 |
| S2 | 3 | 2 | 8 |
| S3 | 2 | 1 | 9 |
| S4 | 2 | 2 | 11 |
Стоимость единицы продукции П1 и П2 соответственно равна 3 и 4 д.е.
Решение. Обозначим через х1 и х2 – количество продукции П1 и П2, входящей в дневной рацион. Тогда общая стоимость рациона составит (д.е.)
F = 3x1 + 4x2. (5)
С учетом необходимого минимума питательных веществ составим систему ограничений. Рацион включает (x1 + 2x2) единиц питательного вещества S1, (3x1 + 2x2) единиц питательного вещества S2, (2x1 + x2) единиц питательного вещества S3 и (2x1 + 2x2) единиц питательного вещества S4. Так как содержание питательных веществ S1, S2, S3, S4 в рационе должно быть не менее 10, 8, 9, 11 единиц, соответственно, то получим систему ограничений неравенств:
x1+2x2 ≥ 10 (6)
3x1+2x2 ≥ 8
2x1+x2 ≥ 9
2x1+2x2 ≥ 11
x1 ≥ 0, x2 ≥ 0
Итак, экономико-математическая модель задачи: составить дневной рацион X=(x1, x2), удовлетворяющий системе ограничений (6), при котором функция (5) принимает минимальное значение.
Сформулируем данную задачу в общей постановке.
Обозначим через xj (j = 1, 2,…, n) – количество единиц j-го продукта в дневном рационе. В рационе используется n видов продуктов. Каждый продукт содержит m питательных веществ в количестве не менее bi (i = 1,2,…,m) единиц, aij – число единиц питательного вещества si в единице продукта j-го вида. Известна стоимость cj единицы j-го продукта. Необходимо составить рацион нужной питательности при минимальных затратах на него.
Экономико-математическая модель примет вид:
F=c1x1+c2x2+…+cnxn→(min) (7)
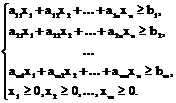 (8)
(8)
Замечание 1. Целевую функцию (7) и систему ограничений неравенств можно записать, используя знак ∑ (суммы).
![]() (9)
(9)
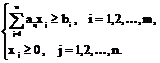 (10)
(10)
Замечание 2. В задаче составления рациона (диеты, кормовой смеси) могут использоваться ограничения не только по необходимому минимуму питательных веществ, но и по минимальному общему весу смеси.
Например. Некоторая фирма имеет возможность купить n различных видов сырья и приготавливать различные виды смесей (продуктов). Каждый вид сырья содержит разное количество питательных веществ. Установлено, что продукция должна удовлетворять некоторым минимальным требованиям с точки зрения питательности (полезности). Необходимо определить количество каждого j-го вида сырья, образующего смесь минимальной стоимости при соблюдении требований к общему расходу смеси и её питательность.
Экономико-математическая модель задачи будет иметь вид:
![]() ,
,
при ограничениях: на общий расход смеси ![]()
на питательность смеси ![]()
на не отрицательность переменных
xj≥0, j=1,2,…n,
где xj – количество j-го сырья в смеси;
n – количество видов сырья;
m – количество питательных веществ;
aij – количество i-го питательного вещества, содержащегося в единице j-го вида сырья;
b1 – минимальное количество i-го питательного вещества, содержащегося в единице смеси;
cj – стоимость единицы сырья j;
q – минимальный общий вид смеси.
Пример №3. В заводской лаборатории создается антифрикционный сплав (оловянистый баббит), который должен содержать: олова - не меньше 15%, сурьмы - не меньше 15%, свинца - около 70%. Есть четыре сплава, процентный состав и цены на которые приведенные в таблице:
| Элементы | Сплав | |||
| 1 | 2 | 3 | 4 | |
| Олово | 12 | 20 | 12 | 20 |
| Сурьма | 12 | 18 | 18 | 14 |
| Свинец | 76 | 62 | 70 | 66 |
| Цена на 1 кг | 3,5 | 5,2 | 4,0 | 4,6 |
Рассчитать количество элементов для сплава каждого вида, необходимое для 1 кг смеси, которая бы обеспечила минимальные затраты.
Решение
Составим экономико-математическую модель задачи.
Обозначим через
x1 – количество сплава 1, кг
x2 – количество сплава 2, кг
x3 – количество сплава 3, кг
x4 – количество сплава 4, кг
Система ограничений по содержанию
12x1 + 20x2 + 12x3 + 20x4 ≥ 15(x1 + x2 + x3 + x4)
12x1 + 18x2 + 18x3 + 14x4 ≥ 15(x1 + x2 + x3 + x4)
76x1 + 62x2 + 70x3 + 66x4 = 70(x1 + x2 + x3 + x4)
Ограничение по количеству
x1 + x2 + x3 + x4 = 1 (кг)
Целевая функция
3,5x1 + 5,2x2 + 4x3 + 4,6x4 → min
Ответ: x1 = 0,25; x2 = 0; x3 = 0,375; x4 = 0,375 (решение можно получить через калькулятор или средствами Excel).
Пример №4. Для сохранения здоровья и работоспособности человек должен в сутки потреблять не менее 63 усл.ед. белков, не менее 147 усл.ед. жиров и не менее 126 усл.ед. углеводов. Для простоты допустим, что имеется всего два вида продуктов и ; стоимость единицы каждого из них равна соответственно 12 и 9 ден.ед. Содержание названных питательных веществ в различных продуктах неодинаково. Предположим, что в единице продукта содержится 9 усл.ед. белков, 7 усл.ед. жиров 9 усл.ед. углеводов; а в единице продукта содержится соответственно 3, 21, 10 усл.ед. тех же питательных веществ. Требуется:
- составить экономико-математическую модель задачи, позволяющую сформировать из продуктов и суточную диету, которая с одной стороны содержала бы белков, жиров и углеводов не менее минимально научно обоснованных норм и вместе с тем требовала бы минимальных затрат;
- решить задачу графическим способом.
x1 - продукт 1, x2 - продукт 2,
Целевая функция: 12x1+9x2 → min
Система ограничений:
9x1+3x2 ≥ 63
7x1+21x2 ≥ 147
9x1+10x2 ≥ 126
Задача о смесях
Постановка задачи: N ингредиентов - y1, y2, y3, y4. В результате смешивания этих ингредиентов в пропорциях g11:g12:g13:g14, g21:g22:g23:g24, g31:g32:g33:g34 и g41:g42:g43:g44 получают смесь n сортов x1, x2, x3, x4. Цена его реализации соответственно s1, s2, s3, s4.Экономико-математическая модель задачи
| Компоненты | Сорта | Объем ресурсов | |||
| x1 | x2 | x3 | x4 | ||
| N1 | g11/Σg1i | g21/Σg2i | g31/Σg3i | g41/Σg4i | y1 |
| N2 | g12/Σg1i | g22/Σg2i | g32/Σg3i | g42/Σg4i | y2 |
| N3 | g13/Σg1i | g23/Σg2i | g33/Σg3i | g43/Σg4i | y3 |
| N4 | g14/Σg1i | g24/Σg2i | g34/Σg3i | g44/Σg4i | y4 |
| Цена | s1 | s2 | s3 | s4 | |
Σg1i = g11 + g12 + g13 + g14
Целевая функция
F(x) = s1x1 + s2x2 + s3x3 + s4x4 → max
Ограничения
x1g11/Σg1i + x2g21/Σg2i + x3g31/Σg3i + x4g41/Σg4i ≤ y1
x1g12/Σg1i + x2g22/Σg2i + x3g32/Σg3i + x4g42/Σg4i ≤ y2
x1g13/Σg1i + x2g23/Σg2i + x3g33/Σg3i + x4g43/Σg4i ≤ y3
x1g14/Σg1i + x2g24/Σg2i + x3g34/Σg3i + x4g44/Σg4i ≤ y4
Назначение сервиса. С помощью данного сервиса можно в онлайн режиме составить математическую модель задачи о смесях и решить ее симплекс-методом или средствами MS Excel.
Пример. Завод выпускает 4 вида полуфабрикатов Bi в количествах: В1 – 400 т, В2 – 250 т, В3 – 350 т и В4 – 100 т.
В результате смешения этих компонентов получают 3 вида продукции Aj. Пропорции смешиваемых полуфабрикатов следующие: для А1 – 2:3:5:2, для А2 – 3:1:2:1, для A3 – 2:2:1:3. Стоимость 1 т продукции Aj составляет: А1 – 12 руб., А2 – 10 руб., А3 – 15 руб.
Составить оптимальный план выпуска продукции по критерию:
а) максимальной стоимости выпущенной продукции;
б) максимального использования полуфабрикатов
Задача об оптимальном составе бетонной смеси
Для приготовления b0 кг бетонной смеси c заданными свойствами используются три вещества Аj (j = 1, 2, 3). В xj кг каждого вещества Аj содержится aijxj кг химического элемента Bi (i = 1, 2). Содержание элемента Bi в смеси должно находиться в пределах от bi1 до bi2 кг. Стоимость 1 кг каждого вещества Aj составляет cj руб.Требуется определить такой состав для приготовления бетонной смеси, при котором общая стоимость израсходованных веществ была бы минимальной.
| A1 | A2 | A3 | Нижняя граница | Верхняя граница |
| a11 | a12 | a13 | b1 | b1 |
| a21 | a22 | a23 | b2 | b2 |
| c1 | c2 | c3 |


