Решение матричной игры
Назначение сервиса. С помощью сервиса в онлайн режиме можно:- определить цену матричной игры (нижнюю и верхнюю границы), проверить наличие седловой точки, найти решение смешанной стратегии, найти минимаксную стратегию игроков;
- записать математическую модель пары двойственных задач линейного программирования, решить матричную игру методами: минимакс, симплекс-метод, графический (геометрический) метод, методом Брауна.
Инструкция. Выберите размерность матрицы, нажмите Далее. В новом диалоговом окне выберите метод решения матричной игры. Пример заполнения. Результаты вычислений оформляются в отчете формата Word.
|
Математической моделью антагонистической игры является матричная игра с матрицей A, в которой ходы (стратегии) игрока A расположены по строкам, а ходы (стратегии) игрока B расположены по столбцам. В самой матрице записаны выигрыши игрока A при соответствующих ходах игроков A и B (отрицательный выигрыш – это проигрыш). |
Алгоритм решения матричной игры
В таблице представлены варианты решения игры, заданной платежной матрицей А.| Наличие седловой точки | Отсутствие седловой точки | |
| Тип стратегии | Чистая стратегия | Смешанная стратегия |
| Метод решения | Решение найдено | 1. Через систему уравнений. 2. Графический метод. 3. Использование симплекс-метода. |
Описание алгоритма:
- На основании анализа платёжной матрицы следует определить, существуют ли в ней доминируемые стратегии, и исключить их.
- Найти верхнюю и нижнюю цены игры и определить, имеет ли данная игра седловую точку (нижняя цена игры должна быть равна верхней цене игры).
- Если седловая точка существует, то оптимальными стратегиями игроков, являющимися решением игры, будут их чистые стратегии, соответствующие седловой точке. Цена игры равна верхней и нижней цены игры, которые равны между собой.
- Если игра не имеет седловой точки, то решение игры следует искать в смешанных стратегиях. Для определения оптимальных смешанных стратегий в играх m × n следует использовать симплекс-метод, предварительно переформулировав игровую задачу в задачу линейного программирования.
Представим алгоритм решения матричной игры графически.
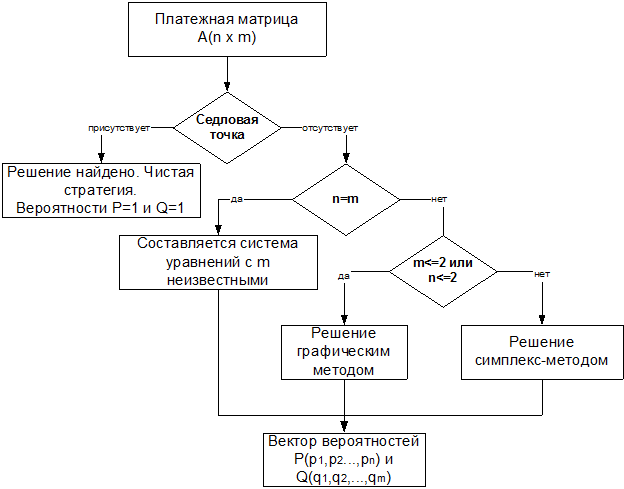
Рисунок - Схема решения матричной игры.
Методы решения матричной игры в смешанных стратегиях
Итак, если седловая точка отсутствует, решение игры проводят в смешанных стратегиях и решают следующими методами:- Решение игры через систему уравнений.
Если задана квадратная матрицаnxn(n=m), то вектор вероятностей можно найти, решив систему уравнений. Этот метод используется не всегда и применим только в отдельных случаях (если матрица2x2, то решение игры получается практически всегда). Если в решении получаются отрицательные вероятности, то данную систему решают симплекс-методом. - Решение игры графическим методом.
В случаях, когдаn=2илиm=2, матричную игру можно решить графически. - Решение матричной игры симплекс-методом.
В этом случае матричная игра сводится к задаче линейного программирования.



