Критерий Гурвица
Критерий Гурвица основан на следующих двух предположениях: «природа» может находиться в самом невыгодном состоянии с вероятностью (1 — y) и в самом выгодном состоянии с вероятностью y, где y — коэффициент доверия. Если результат hji — прибыль, полезность, доход и т.п., то критерий Гурвица записывается так:W = max[ymax[hji]+(1-y)min[hji]]
Когда целевая функция представляет затраты (потери), то:
W = min[ymin[hji]+(1-y)max[hji]]
Назначение сервиса. С помощью онлайн калькулятора выбирается оптимальная стратегия по критерию Гурвица. Результаты вычислений оформляются в отчете формата Word (см. Пример оформления).
Инструкция Для расчета и оформления решения в формате Word и Excel необходимо выбрать
Критерий Гурвица устанавливает баланс между случаями крайнего пессимизма и крайнего оптимизма путем взвешивания обоих способов поведения соответствующими весами (1 — y) и y, где 0<y<1. Значение y от 0 до 1 может определяться в зависимости от склонности лица, принимающего решение, к пессимизму или к оптимизму. При отсутствии ярко выраженной склонности y = 0,5 представляется наиболее разумной.
Пример. Исходные данные:
| 8 | 4 | 6 | 20 |
| 7 | 7 | 7 | 7 |
| 6 | 12 | 8 | 10 |
По критерию Вальда за оптимальную принимается чистая стратегия, которая в наихудших условиях гарантирует максимальный выигрыш, т.е.
a = max(min aij)
Критерий Вальда ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации.
| Ai | П1 | П2 | П3 | П4 | min(aij) |
| A1 | 8 | 4 | 6 | 20 | 4 |
| A2 | 7 | 7 | 7 | 7 | 7 |
| A3 | 6 | 12 | 8 | 10 | 6 |
Вывод: выбираем стратегию N=2.
Критерий Севиджа.
Критерий минимального риска Севиджа рекомендует выбирать в качестве оптимальной стратегии ту, при которой величина максимального риска минимизируется в наихудших условиях, т.е. обеспечивается:
a = min(max rij)
Критерий Сэвиджа ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации.
Находим матрицу рисков.
Риск – мера несоответствия между разными возможными результатами принятия определенных стратегий. Максимальный выигрыш в j-м столбце bj = max(aij) характеризует благоприятность состояния природы.
1. Рассчитываем 1-й столбец матрицы рисков.
r11 = 8 - 8 = 0; r21 = 8 - 7 = 1; r31 = 8 - 6 = 2;
2. Рассчитываем 2-й столбец матрицы рисков.
r12 = 12 - 4 = 8; r22 = 12 - 7 = 5; r32 = 12 - 12 = 0;
3. Рассчитываем 3-й столбец матрицы рисков.
r13 = 8 - 6 = 2; r23 = 8 - 7 = 1; r33 = 8 - 8 = 0;
4. Рассчитываем 4-й столбец матрицы рисков.
r14 = 20 - 20 = 0; r24 = 20 - 7 = 13; r34 = 20 - 10 = 10
| Ai | П1 | П2 | П3 | П4 |
| A1 | 0 | 8 | 2 | 0 |
| A2 | 1 | 5 | 1 | 13 |
| A3 | 2 | 0 | 0 | 10 |
| Ai | П1 | П2 | П3 | П4 | max(aij) |
| A1 | 0 | 8 | 2 | 0 | 8 |
| A2 | 1 | 5 | 1 | 13 | 13 |
| A3 | 2 | 0 | 0 | 10 | 10 |
Вывод: выбираем стратегию N=1.
Критерий Гурвица.
Критерий Гурвица является критерием пессимизма - оптимизма. За оптимальную принимается та стратегия, для которой выполняется соотношение:
max(si)
где si = y min(aij) + (1-y)max(aij)
При y = 1 получим критерий Вальде, при y = 0 получим – оптимистический критерий (максимакс).
Критерий Гурвица учитывает возможность как наихудшего, так и наилучшего для человека поведения природы. Как выбирается y? Чем хуже последствия ошибочных решений, тем больше желание застраховаться от ошибок, тем y ближе к 1.
Рассчитываем si.
s1 = 0.5•4+(1-0.5)•20 = 12
s2 = 0.5•7+(1-0.5)•7 = 7
s3 = 0.5•6+(1-0.5)•12 = 9
| Ai | П1 | П2 | П3 | П4 | min(aij) | max(aij) | y min(aij) + (1-y)max(aij) |
| A1 | 8 | 4 | 6 | 20 | 4 | 20 | 12 |
| A2 | 7 | 7 | 7 | 7 | 7 | 7 | 7 |
| A3 | 6 | 12 | 8 | 10 | 6 | 12 | 9 |
Вывод: выбираем стратегию N=1.
Обобщенный критерий Гурвица.
Данный критерий является некоторым обобщением критериев крайнего пессимизма и крайнего оптимизма и также представляет собой частный случай обобщенного критерия Гурвица относительно выигрышей при следующем допущении:
λ1=1-λ, λ2=λ3=…=λn-1=0, λn=λ, где 0 ≤ λ ≤ 1
Тогда показатель эффективности стратегии Ai по Гурвицу есть:
Gi=(1-λ)min aij + λmax aij
Оптимальной стратегией Ai0 считается стратегия с максимальным значением показателя эффективности.
Строим вспомогательную матрицу B, полученную путем упорядочивания показателей доходностей в каждой строке.
Подход пессимиста. λ выбирается из условия невозрастания среднего:
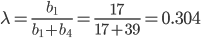
G1 = 0.304 • 4+(1-0.304) • 20 = 15.143; G2 = 0.304 • 7+(1-0.304) • 7 = 7; G3 = 0.304 • 6+(1-0.304) • 12 = 10.179;
Подход оптимиста. λ выбирается из условия неубывания среднего:
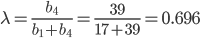
G1 = 0.696 • 4+(1-0.696) • 20 = 8.857; G2 = 0.696 • 7+(1-0.696) • 7 = 7; G3 = 0.696 • 6+(1-0.696) • 12 = 7.821
| Ai | П1 | П2 | П3 | П4 | min(aij) | max(aij) | Подход пессимиста | Подход оптимиста |
| A1 | 4 | 6 | 8 | 20 | 4 | 20 | 15.14 | 8.86 |
| A2 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 |
| A3 | 6 | 8 | 10 | 12 | 6 | 12 | 10.18 | 7.82 |
Вывод: выбираем стратегию N=1.
Оптимальные стратегии по обобщенному критерию Гурвица.
b = 17 + 21 + 25 + 39 = 102
Показатели эффективности по Гурвицу.
Подход пессимиста
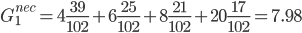
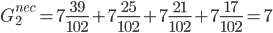
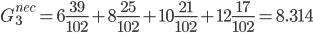
Подход оптимиста
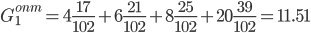
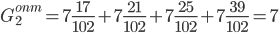
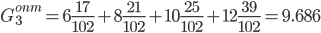
Таким образом, в результате решения статистической игры по различным критериям чаще других рекомендовалась стратегия A1.

