Биматричные игры
В играх с ненулевой суммой в выигрыше или проигрыше могут оказаться все участники игры. Биматричная игра – это конечная игра двух игроков с ненулевой суммой. В этом случае для каждой игровой ситуации AiBj каждый из игроков имеет свой выигрыш aij для первого игрока и bij– для второго игрока. К биматричной игре сводится, например, поведение производителей на рынках несовершенной конкуренции. С помощью онлайн-калькулятора можно найти решение биматричной игры, а также ситуации оптимальные по Парето и ситуации устойчивые по Нэшу.
Рассмотрим конфликтную ситуацию, в которой каждый из двух участников имеет следующие возможности для выбора своей линии поведения:
- игрок А – может выбрать любую из стратегий А1,…,Аm,
- игрок В – любую из стратегий В1,…,Вn.
При этом их совместный выбор оценивается вполне определённо: если игрок А выбрал i-ю стратегию Аi, а игрок В – k-ю стратегию Вk, то в итоге выигрыш игрока А будет равен некоторому числу aik, а выигрыш игрока В некоторому, вообще говоря, другому числу bik.
Последовательно перебирая все стратегии игрока А и все стратегии игрока В, мы сможем заполнить их выигрышами две таблицы.
Первая из таблиц описывает выигрыш игрока А, а вторая – выигрыш игрока В. Обычно эти таблицы записывают в виде матрицы.
Здесь А – платёжная матрица игрока А, В – платёжная матрица игрока В.
Таким образом, в случае, когда интересы игроков различны (но не обязательно противоположны) получаются две платёжные матрицы: одна – матрица выплат игроку А, другая – матрица выплат игроку В. Поэтому совершенно естественно звучит название, которое обычно присваивается подобной игре – биматричная.
Равновесие Нэша – равновесие, когда каждый участник игры выбирает стратегию, которая является для него оптимальной при условии, что остальные участники игры придерживаются определенной стратегии.
Равновесие Нэша не всегда является наиболее оптимальным для участников. В этом случае говорят, что равновесие не является Парето-оптимальным.
Чистая стратегия – определенная реакция игрока на возможные варианты поведения других игроков.
Смешанная стратегия – вероятностная (не определенная точно) реакция игрока на поведение других игроков.
Пример №1. Борьба за рынки сбыта.
Фирма а намерена сбыть партию товара на одном из двух рынков, контролируемых более крупной фирмой b. С этой целью она проводит подготовительную работу, связанную с определенными затратами. Если фирма b разгадает, на каком из рынков фирма а будет продавать свой товар, она примет контрмеры и воспрепятствует "захвату" рынка (этот вариант означает поражение фирмы а); если нет, то фирма а одерживает победу. Предположим, что для фирмы а проникновение на первый рынок более выгодно, чем проникновение на второй, но и борьба на первом рынке требует от нее больших средств. Например, победа фирмы а на первом рынке приносит ей вдвое большую прибыль, чем победа на втором, но зато поражение на первом рынке полностью ее разоряет.
Составим математическую модель этого конфликта, считая фирму а игроком 1 и фирму b игроком 2. Стратегии игрока 1: А1 – проникновение на рынок 1, А2 – проникновение на рынок 2; стратегии игрока 2: В1 – контрмеры на рынке 1, В2 – контрмеры на рынке 2. Пусть для фирмы а ее победа на 1-м рынке оценивается в 2 единицы, а победа на 2-м рынке – в 1 единицу; поражение фирмы а на 1-м рынке оценивается в -10, а на 2-м в -1. Для фирмы b ее победа составляет соответственно 5 и 1 единицу, а поражение -2 и -1. Получаем в итоге биматричную игру Г с матрицами выигрышей
.
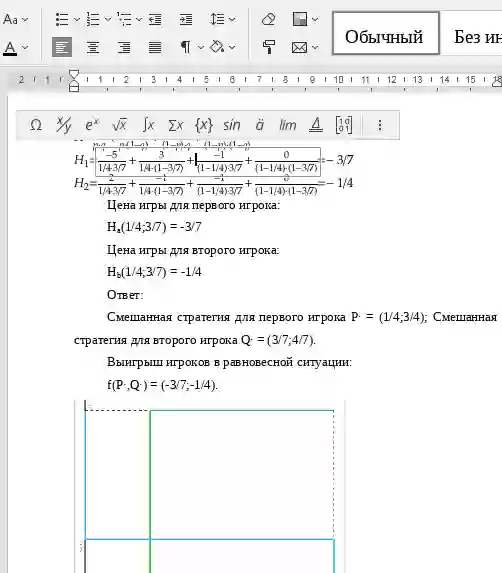
По теореме эта игра может иметь либо чистые, либо вполне смешанные ситуации равновесия. Ситуаций равновесия в чистых стратегиях здесь нет. Убедимся теперь, что данная игра имеет вполне смешанную ситуацию равновесия. Находим 
, 
.
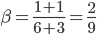Итак, рассматриваемая игра имеет единственную ситуацию равновесия (x0;y0), где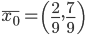 
, 
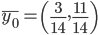. Она может быть реализована при многократном повторении игры (то есть при многократном воспроизведении описанной ситуации) следующим образом: фирма а должна использовать чистые стратегии 1 и 2 с частотами 2/9 и 7/9, а фирма b – чистые стратегии 1 и 2 с частотами 3/14 и 11/14. Любая из фирм, отклонившись от указанной смешанной стратегии, уменьшает свой ожидаемый выигрыш.
Пример №2. Найти ситуации оптимальные по Парето и ситуации устойчивые по Нэшу для биматричной игры.
Пример №3. Имеются 2 фирмы: первая может произвести одно из двух изделий А1 и А2, вторая – одно из двух изделий B1, B2. Если первая фирма произведет продукцию Ai (i = 1, 2), а вторая - Bj (j = 1, 2), то прибыль этих фирм (зависящая от того, являются ли эти изделия взаимодополняющими или конкурирующими), определяется таблицей №1:
| В1 | В2 | |
| А1 | (5, 6) | (3, 2) |
| А2 | (2, 1) | (5, 3) |
