Смешанные стратегии
В общем случае V* ≠ V* - седловой точки не существует. Оптимальное решение в чистых стратегиях также не существует. Однако, если расширить понятие чистой стратегии введением понятия смешанной стратегии, то удаётся реализовать алгоритм нахождения оптимального решения не вполне определённой игровой задачи. В такой ситуации предлагается использование статистического (вероятностного) подхода к нахождению оптимального решения антагонистической игры. Для каждого игрока, наряду с данным набором возможных для него стратегий, вводится неизвестный вектор вероятностей (относительных частот), с которыми следует применять ту или иную стратегию.Обозначим вектор вероятностей (относительных частот) выбора заданных стратегий игрока A следующим образом:
P = (p1, p2,…, pm),
где pi≥ 0, p1 + p2 +…+ pm= 1. Величина pi называется вероятностью (относительной частотой) применения стратегии Ai.
Аналогично для игрока B вводится неизвестный вектор вероятностей (относительных частот) имеет вид:
Q = (q1, q2,…, qn),
где qj≥ 0, q1 + q2 +…+ qn = 1. Величина qj называется вероятностью (относительной частотой) применения стратегии Bj. Совокупность (комбинация) чистых стратегий A1, A2, …Am и B1, B2, …Bn в сочетании с векторами вероятностей выбора каждой из них называются смешанными стратегиями.
Основной теоремой в теории конечных антагонистических игр является Теорема фон Неймана: каждая конечная матричная игра имеет, по крайней мере, одно оптимальное решение, возможно, среди смешанных стратегий.
Из этой теоремы следует, что не вполне определённая игра имеет хотя бы одно оптимальное решение в смешанных стратегиях. В таких играх решением будет пара оптимальных смешанных стратегий P* и Q*, таких, что если один из игроков придерживается своей оптимальной стратегии, то и другому игроку не выгодно отклоняться от своей оптимальной стратегии.
Средний выигрыш игрока A определяется математическим ожиданием:
![]()
Если вероятность (относительная частота) применения стратегии отлична от нуля, то такая стратегия называется активной.
Стратегии P*, Q* называются оптимальными смешанными стратегиями, если MA(P, Q*) ≤ MA(P*, Q*) ≤ MA(P*, Q) (1)
В этом случае MA(P*, Q*) называется ценой игры и обозначается через V (V* ≤ V ≤ V*). Первое из неравенств (1)означает, что отклонение игрока A от своей оптимальной смешанной стратегии при условии, что игрок B придерживается своей оптимальной смешанной стратегии, приводит к уменьшению среднего выигрыша игрока A. Второе из неравенств означает, что отклонение игрока B от своей оптимальной смешанной стратегии при условии, что игрок A придерживается своей оптимальной смешанной стратегии, приводит к увеличению среднего проигрыша игрока B.
В общем случае подобные задачи успешно решаются этим калькулятором.
Пример.
| 4 | 7 | 2 |
| 7 | 3 | 2 |
| 2 | 1 | 8 |
1. Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях.
Считаем, что игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I.
| Игроки | B1 | B2 | B3 | a = min(Ai) |
| A1 | 4 | 7 | 2 | 2 |
| A2 | 7 | 3 | 2 | 2 |
| A3 | 2 | 1 | 8 | 1 |
| b = max(Bi) | 7 | 7 | 8 |
Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(ai) = 2, которая указывает на максимальную чистую стратегию A1.
Верхняя цена игры b = min(bj) = 7. Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры находится в пределах 2 ≤ y ≤ 7. Находим решение игры в смешанных стратегиях. Объясняется это тем, что игроки не могут объявить противнику свои чистые стратегии: им следует скрывать свои действия. Игру можно решить, если позволить игрокам выбирать свои стратегии случайным образом (смешивать чистые стратегии).
2. Проверяем платежную матрицу на доминирующие строки и доминирующие столбцы.
В платежной матрице отсутствуют доминирующие строки и доминирующие столбцы.
3. Находим решение игры в смешанных стратегиях.
Запишем систему уравнений.
Для игрока I
4p1+7p2+2p3 = y
7p1+3p2+p3 = y
2p1+2p2+8p3 = y
p1+p2+p3 = 1
Для игрока II
4q1+7q2+2q3 = y
7q1+3q2+2q3 = y
2q1+q2+8q3 = y
q1+q2+q3 = 1
Решая эти системы методом Гаусса, находим:
y = 41/34
p1 = 29/68 (вероятность применения 1-ой стратегии).
p2 = 4/17 (вероятность применения 2-ой стратегии).
p3 = 23/68 (вероятность применения 3-ой стратегии).
Оптимальная смешанная стратегия игрока I: P = (29/68; 4/17; 23/68)
q1 = 6/17 (вероятность применения 1-ой стратегии).
q2 = 9/34 (вероятность применения 2-ой стратегии).
q3 = 13/34 (вероятность применения 3-ой стратегии).
Оптимальная смешанная стратегия игрока II: Q = (6/17; 9/34; 13/34)
Цена игры: y = 41/34
Пример №2. Матричную игру 2х2 решить в смешанных стратегиях:
1) аналитически (для игрока А); геометрически (для игрока В)
2) провести моделирование результатов игры с помощью таблицы равномерно распределенных случайных чисел, разыграв 30 партий; определить относительные частоты использования чистых стратегий каждым игроком и средний выигрыш, сравнив результаты с полученными теоретически в п.1.
Игра задана платежной матрицей: 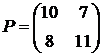 .
.
Решение:
1. Найдем аналитически оптимальную стратегию игрока А и соответствующую цену игры Х*(р1, р2), n.
Так как Х* - оптимальная, то она должна гарантировать средний выигрыш игроку А, равный цене игры при любом поведении игрока В:
для стратегии В1: 10p1 + 8p2 = v;
для стратегии В2: 7p1+11p2 = v.
С учетом того, что сумма компонентов смешанной стратегии равна 1, получаем систему уравнений:
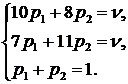
Вычтем из первого уравнения второе: 3p1 - 3p2 = 0 или p1 = p2.Значит:
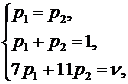
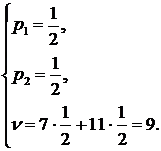
Итак: 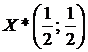 , n = 9.
, n = 9.
Найдем геометрически оптимальную смешанную стратегию игрока В: Y*(q1, q2).
Стратегию А1 изобразим точками с ординатами 10 и 7 на прямых В1 и В2 соответственно. Стратегию А2 - точками с ординатами 8 и 11 (см. рис. 1).
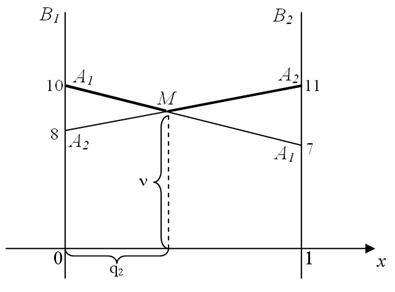
Рис. 1. Геометрическая интерпретация матричной игры для игрока В
Каждой точке на отрезке [0; 1] соответствует смешанная стратегия игрока В. Среди них оптимальной будет та, которая определяется самой низкой точкой ломанной А1МА2, т.е. точкой М. Для нахождения компонентов оптимальной стратегии игрока В надо найти координаты точки М, причем если М (х, у), то q1 = 1 - х, q2 = х, n = y. Для этого найдем уравнения прямых А1А1 и А2А2, воспользовавшись уравнением прямой, проходящей через две точки:
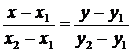 .
.
Так как А1(0; 10) и А1(1; 7), то
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Т.е. уравнение прямой А1А1 имеет вид: 3x + y - 10 = 0.
Так как А2(0; 8) и А2(1; 11), то
![]() ,
, ![]() , 3x = y-8, 3x-y + 8=0.
, 3x = y-8, 3x-y + 8=0.
Т.е. уравнение прямой А2А2 имеет вид: 3x-y + 8 = 0.
Найдем координаты точки М, решив систему уравнений прямых А1А1 и А2А2:
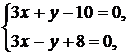
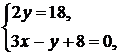
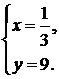
Итак, 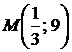 , значит n = 9,
, значит n = 9, 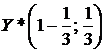 или
или 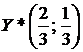 .
.
Ответ: 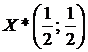 ,
, 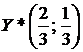 , n = 9.
, n = 9.
2. Проведем моделирование результатов решения с помощью таблицы равномерно распределенных случайных чисел. Для 30 партий хватит 60 чисел, на основе которых будут выбираться стратегии игроками. Используемые случайные числа сгенерированы в MS Excel функцией =СЛЧИС(). В приложении достаточно много чисел, но использовать для моделирования можно любые 60, выбранные произвольно с любого места таблицы. Мы возьмем первые числа.
| 0,02988 | 0,12558 | 0,25974 | 0,17641 | 0,00937 | 0,52264 | 0,08086 | 0,84858 | 0,99427 | 0,49452 |
| 0,61109 | 0,49042 | 0,61076 | 0,65834 | 0,25579 | 0,80641 | 0,07675 | 0,84419 | 0,18268 | 0,29702 |
| 0,76606 | 0,95854 | 0,20704 | 0,45154 | 0,27367 | 0,56261 | 0,30037 | 0,96485 | 0,47252 | 0,55084 |
| 0,73868 | 0,56421 | 0,07183 | 0,99420 | 0,11184 | 0,80524 | 0,42897 | 0,45031 | 0,05350 | 0,67078 |
| 0,94483 | 0,25710 | 0,39190 | 0,72491 | 0,88888 | 0,03791 | 0,50773 | 0,63034 | 0,94091 | 0,80165 |
| 0,41647 | 0,88664 | 0,83519 | 0,46930 | 0,39285 | 0,34159 | 0,77252 | 0,65987 | 0,48750 | 0,79735 |
| 0,51314 | 0,22625 | 0,06211 | 0,39299 | 0,84336 | 0,80859 | 0,52694 | 0,73306 | 0,36874 | 0,93390 |
| 0,71749 | 0,46727 | 0,18182 | 0,45791 | 0,08667 | 0,58570 | 0,75495 | 0,68645 | 0,90270 | 0,87484 |
| 0,99401 | 0,82235 | 0,89122 | 0,33631 | 0,42694 | 0,37053 | 0,70413 | 0,59805 | 0,40425 | 0,96181 |
| 0,41244 | 0,24426 | 0,37553 | 0,09464 | 0,56208 | 0,68889 | 0,59503 | 0,92378 | 0,03108 | 0,33182 |
Заполним расчетную таблицу:
| Номер партии | Случайное число игрока А | Стратегия игрока А (А1: < 0,5) | Случайное число игрока В | Стратегия игрока В (В1: < 0,667) | Выигрыш А | Накопленный выигрыш А | Средний выигрыш А (цена игры) |
| 1 | 0,029 | А1 | 0,125 | В1 | 10 | 10 | 10,000 |
| 2 | 0,611 | А2 | 0,490 | В1 | 8 | 18 | 9,000 |
| 3 | 0,766 | А2 | 0,958 | В2 | 11 | 29 | 9,667 |
| 4 | 0,738 | А2 | 0,564 | В1 | 8 | 37 | 9,250 |
| 5 | 0,944 | А2 | 0,257 | В1 | 8 | 45 | 9,000 |
| 6 | 0,416 | А1 | 0,886 | В2 | 7 | 52 | 8,667 |
| 7 | 0,513 | А1 | 0,226 | В1 | 10 | 62 | 8,857 |
| 8 | 0,717 | А2 | 0,467 | В1 | 8 | 70 | 8,750 |
| 9 | 0,994 | А2 | 0,822 | В2 | 11 | 81 | 9,000 |
| 10 | 0,412 | А1 | 0,244 | В1 | 10 | 91 | 9,100 |
| 11 | 0,259 | А1 | 0,176 | В1 | 10 | 101 | 9,182 |
| 12 | 0,610 | А2 | 0,658 | В1 | 8 | 109 | 9,083 |
| 13 | 0,207 | А1 | 0,451 | В1 | 10 | 119 | 9,154 |
| 14 | 0,071 | А1 | 0,994 | В2 | 7 | 126 | 9,000 |
| 15 | 0,391 | А1 | 0,724 | В2 | 7 | 133 | 8,867 |
| 16 | 0,835 | А2 | 0,469 | В1 | 11 | 144 | 9,000 |
| 17 | 0,062 | А1 | 0,392 | В1 | 10 | 154 | 9,059 |
| 18 | 0,181 | А1 | 0,457 | В1 | 10 | 164 | 9,111 |
| 19 | 0,891 | А2 | 0,336 | В1 | 8 | 172 | 9,053 |
| 20 | 0,375 | А1 | 0,094 | В1 | 10 | 182 | 9,100 |
| 21 | 0,009 | А1 | 0,522 | В1 | 10 | 192 | 9,143 |
| 22 | 0,255 | А1 | 0,806 | В2 | 7 | 199 | 9,045 |
| 23 | 0,273 | А1 | 0,562 | В1 | 10 | 209 | 9,087 |
| 24 | 0,111 | А1 | 0,805 | В2 | 7 | 216 | 9,000 |
| 25 | 0,888 | А2 | 0,037 | В1 | 8 | 224 | 8,960 |
| 26 | 0,392 | А1 | 0,341 | В1 | 10 | 234 | 9,000 |
| 27 | 0,843 | А2 | 0,808 | В2 | 11 | 245 | 9,074 |
| 28 | 0,086 | А1 | 0,585 | В1 | 10 | 255 | 9,107 |
| 29 | 0,426 | А1 | 0,370 | В1 | 10 | 265 | 9,138 |
| 30 | 0,562 | А2 | 0,688 | В2 | 11 | 276 | 9,200 |
Частоты использования игроками своих чистых стратегий соответственно равны:
Х(18/30;12/30), Y(21/30; 9/30) или
Х(0,6; 0,4), Y(0,7; 0,3)
Сравнивая с теоретическими оптимальными стратегиями Х*(0,5; 0,5) и Y*(0,67; 0,33) можно сделать вывод, что результаты моделирования достаточно близко им соответствуют даже для небольшого количества партий.
Пример №2. Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях.
| Игроки | B1 | B2 | a = min(Ai) |
| A1 | 4 | 5 | 4 |
| A2 | 7 | 3 | 3 |
| b = max(Bi ) | 7 | 5 | 0 |
Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(ai) = 4, которая указывает на максимальную чистую стратегию A1. Верхняя цена игры b = min(bj) = 5.
Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры находится в пределах 4 ≤ y ≤ 5. Находим решение игры в смешанных стратегиях.
Запишем систему уравнений.
Для игрока I
4p1+7p2 = y
5p1+3p2 = y
p1+p2 = 1
Для игрока II
4q1+5q2 = y
7q1+3q2 = y
q1+q2 = 1
Решая эти системы методом Гаусса, находим:
y = 43/5
p1 = 4/5 (вероятность применения 1-ой стратегии).
p2 = 1/5 (вероятность применения 2-ой стратегии).
Оптимальная смешанная стратегия игрока I: P = (4/5; 1/5)
q1 = 2/5 (вероятность применения 1-ой стратегии).
q2 = 3/5 (вероятность применения 2-ой стратегии).
Оптимальная смешанная стратегия игрока II: Q = (2/5; 3/5)
Цена игры
y = 43/5

