Решение игры в смешанных стратегиях геометрическим методом
Пусть игра задана платежной матрицей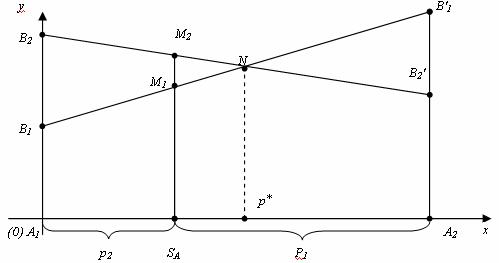
. По оси абсцисс отложим единичный отрезок А1А2, где точка А1 (0, 0) изображает стратегию А1, А2 (1, 0) –
стратегию А2, а каждая промежуточная точка SA этого отрезка изображает смешанную стратегию первого игрока PA = (p1, p2), где p1– расстояние от точки SA
до A2, p2–расстояние от точки SA до A1. Выигрыш игрока A будем откладывать на вертикальных отрезках.
, т.е. y=a11+x(a21-a11),
тогда при x = p2 получим
y = a11 + p2a21 – p2a11 = a11(1-p2) + p2a21 = a11p1 + a21p2
Случай 2. Если игрок B применяет стратегию В2, то аналогично откладываем отрезки а12 и а22 и получаем отрезок В2В2′. Ордината любой точки М2 отрезка В2В2′ – выигрыш игрока A, если A применяет смешанную стратегию SA, а B – стратегию В2.
Построим нижнюю границу выигрыша игрока А – ломаную В1 NВ2′. Ординаты точек этой ломаной показывают минимальные выигрыши игрока А при использовании им любой смешанной стратегии. Оптимальное решение игры определяет точка N, в которой выигрыш игрока А принимает наибольшее значение. Ордината точки N равна цене игры. Проекция этой точки на ось ОХ показывает оптимальную стратегию (р1, р2).
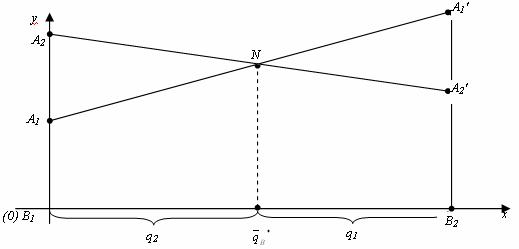
Аналогично находится оптимальная стратегия Q = (q1 , q2) игрока B, только в соответствии с принципом минимакса надо находить верхнюю границу выигрыша, т. е. строить ломаную А2NА1′ и брать точку N с наименьшей ординатой.
Абсцисса точки N определяет оптимальную стратегию игрока B, т. е. Q = (q1 , q2).
Пример №1. Решить игру, заданную платежной матрицей 
, графоаналитическим способом.
Решение. Нижняя цена игры α = 1,5, верхняя цена игры β = 2. Так как α≠β, седловой точки нет. Так как a1 = 1,5, a21 = 2 строим точки B1(0;1,5) и B2(1;2), соединяем их отрезком. Так как a21 = 3, a22 = 1 строим точки B2(0;3) и B2’(1;1), соединяем их отрезком.
, т. е. y = 0,5x + 1,5;
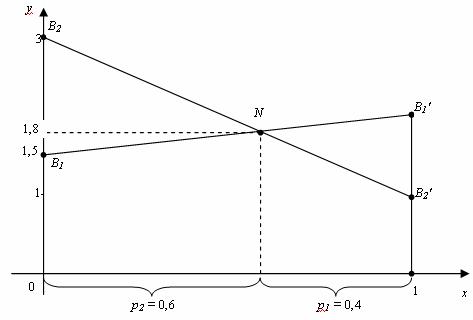
уравнение В2В2′:
, т. е. y = 3-2x.
Найдем точку N пересечения прямых В1В1′ и В2В2′, для чего решим систему уравнений:
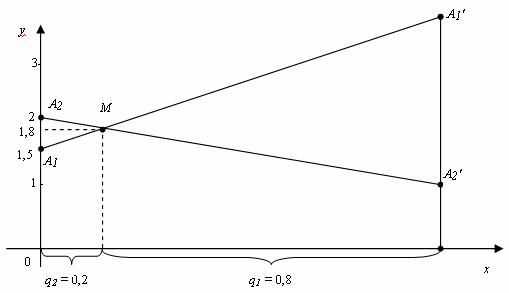
Аналогично строим точки А1(0; 1,5) и А1′(1;3), А2(0; 2) и А2′(1; 1) и находим точку M пересечения прямых А1А1′ и А2А2′.
Пример №2. Решить матричную игру, в которой один из игроков имеет две чистые стратегии, или игру, которая сводится к таковой после отбрасывания доминируемых строк и столбцов. Для нахождения цены игры и оптимальной стратегии игрока, имеющего две чистые стратегии, применяется графический метод. Для другого игрока оптимальная стратегия ищется исходя из свойств оптимальных стратегий и цены игры. Список рекомендуемых для контрольной работы задач прилагается.
Перейти к онлайн решению своей задачи
Решение игры 2×2
Покажем на примере платёжной матрицы размерностью 2×2 реализацию алгоритма построения оптимального решения игровой задачи в смешанных стратегиях.Пример №3. Найдем решение матричной игры
V* = -1, V* = 1, V* ≠V* - решения в чистых стратегиях не существует.
Припишем строкам платёжной матрицы неизвестные вероятности p1 и p2 (вероятности выбора стратегий A1 и A2) соответственно:
.
Поскольку p1 + p2 =1 → p2 = 1 - p1. Обозначим p1 = p, тогда p2 =1 - p. В результате получим:
Умножим столбец 
поэлементно на 1-й столбец и, сложив произведения, получим - математическое ожидание (среднее значение) выигрыша первого игрока A, при условии, что второй игрок B следует первой стратегии.
M1(p) = 1∙p + (-1)(1-p) = 2p-1
Умножим столбец поэлементно на 2-й столбец и, сложив произведения, получим линейную зависимость - математическое ожидание (средний выигрыш) игрока A при применении игроком B второй стратегии
M2(p) = (-1)∙p + 1(1-p) = -2p+1
Поскольку мы разыскиваем оптимальное решение первого игрока A, которое не должно зависеть от выбора стратегий вторым игроком B, приравняем полученные зависимости средних выигрышей:
2p-1 = -2p+1
Отсюда, p= ½, 1-p = ½, то есть оптимальная смешанная стратегия игрока A - это P = (½, ½ ) (каждую из стратегий надо применять с относительной частотой ½). Подставив p=½ в любую из зависимостей Mi(p), i=1,2 найдем цену игры:
V=Mi(½) = 0.
Теперь припишем столбцам вероятности q1 и q2 соответственно, а поскольку:
q1 + q2 =1 →q2 = 1 - q1. Обозначим q1 = q, тогда q2 =1 - q. В результате получим:
.
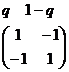Умножив строку (q, 1-q) на 1-ю строку и сложив произведения, получим линейную зависимость - математическое ожидание:
W1(q) = 1· q + (-1) ·(1-q) = 2q - 1
Это средний выигрыш игрока A (равный проигрышу игрока B) при применении игроком A 1-й стратегии.
Умножив строку (q, 1-q) на 2-ю строку и сложив произведения, получим линейную зависимость - математическое ожидание:
W2 = (-1) · q + 1· (1-q) = -2q + 1
Это средний выигрыш игрока A (равный проигрышу игрока B) при применении игроком A 2-й стратегии.
Приравняем полученные зависимости:
2q -1 = -2q + 1
Отсюда, q = ½, 1 - q = ½, то есть оптимальная смешанная стратегия игрока B - это Q = (½, ½) (каждую из стратегий надо применять с относительной частотой ½).
Решение о конкретном выборе одной из своих стратегий каждый из игроков может принимать с помощью подбрасывания монеты или бинарного датчика случайных чисел.
Как показывает приведённый пример, оптимальные смешанные стратегии сравнительно легко находятся для игр, имеющих небольшую размерность платёжной матрицы (небольшие m и n), т.е. для игр, в которых каждый из игроков имеет небольшое число стратегий. В то же время для игр, имеющих большую размерность, поиск решения становится достаточно сложным. Поэтому до построения оптимального решения в смешанных стратегиях проводят предварительный анализ платёжной матрицы на предмет её упрощения, исключения из неё дублирующих и доминируемых стратегий, что позволяет существенно упростить поиск решения игровой задачи в смешанных стратегиях.
Решение игр вида 2хn и mх2
Графо-аналитический метод.У таких игр всегда имеется решение, содержащее не более двух активных стратегий для каждого из игроков. Если найти эти активные стратегии, то игра 2 х n или m х 2 сводится к игре 2 х 2, которую мы уже умеем решать. Поэтому игры 2 х n и m х 2 решают обычно графоаналитическим методом.
Рассмотрим решение матричной игры на примере.
Пример №4. 
Решение.
| αi | ||||
| 1 | 4 | 7 | 1 | |
| 6 | 3 | 2 | 2 | |
| βj | 6 | 4 | 7 | 2 4 |
α=2, β=4, α≠β, поэтому игра не имеет седловой точки, и решение должно быть в смешанных стратегиях.
1. Строим графическое изображение игры.
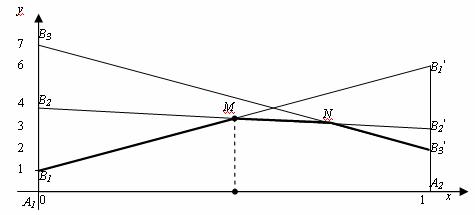
2. Выделяем нижнюю границу выигрыша В1М N В3′ и находим наибольшую ординату этой нижней границы, ординату точки М, которая равна цене игры γ.
3. Определяем пару стратегий, пересекающихся в точке оптимума М.
В этой точке пересекаются отрезки В2В2′ и В1В1′, соответствующие стратегиям В1 и В2 игрока B. Следовательно, стратегию В3 ему применять невыгодно. Исключаем из матрицы третий столбец и решаем игру 2 x 2 аналитически:
; 
; 
.
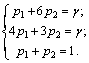
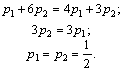
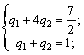
Ответ: γ = 7/2; PA = (1/2; 1/2); QB = (1/6; 5/6; 0).
Перейти к онлайн решению своей задачи
Правила решения игры mx2
- строится графическое изображение игры;
- выделяется нижняя граница выигрыша и находится наибольшая ордината нижней границы, которая равна цене игры γ;
- определяется пара стратегий, пересекающихся в точке оптимума M. Эти стратегии являются активными стратегиями игрока B. Если в точке оптимума пересекаются более двух стратегий, то в качестве активных стратегий может быть выбрана любая пара из них;
- решается полученная игра 2x2.
♦ выделяется верхняя граница выигрыша, и на ней находится точка оптимума с наибольшей ординатой.
Пример №5
Решение.
| αi | |||
| 0,4 | 1,0 | 0,4 | |
| 0,5 | 0,5 | 0,5 | |
| 1,0 | 0,3 | 0,3 | |
| 0,8 | 0,3 | 0,3 | |
| βj | 1,0 | 1,0 | 0,5 / 1,0 |
1. строим графическое изображение игры относительно игрока В.
Если А применяет А1, то при использовании игроком В стратегии В1 выигрыш игрока А равен 0,4, а выигрыш А при стратегии В2 равен 1,0, поэтому на перпендикулярах строим такие отрезки. Видно, что стратегия А4 заведомо невыгодная по сравнению со стратегией А3 (выигрыш меньше).
2. Выделяем верхнюю границу выигрыша А3NА1′; точка с наименьшей ординатой – N.
3. В этой точке пересекаются отрезки А1А1′ и А3А3′, соответствующие активным стратегиям А1 и А3. Стратегия А2 не является активной, поэтому из матрицы исключаем вторую и четвертую строки:
.
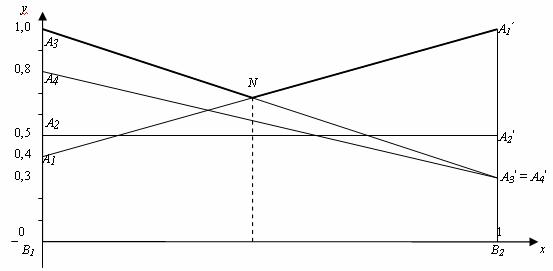
4. решаем игру:
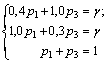
13p3 = 6; p3 =6/13; p1 = 7/13
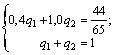
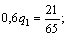
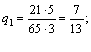
Ответ: γ = 44/65; PA = (7/13; 0; 6/13; 0); QB = (7/13; 6/13).
Примечание: Игроку А не выгодно отклоняться от спектра своих активных стратегий.
Перейти к онлайн решению своей задачи
Модель сотрудничества и конкуренции
Рассмотреть матричную игру как модель сотрудничества и конкуренции. Найти графически решение игры. Указать, как проявляется конкуренция между игроками и сотрудничество между ними.Решение: Седловой точки нет. Обозначим искомую оптимальную стратегию первого игрока (х, 1-х). Это вектор-столбец, который мы записываем для удобства в виде строки.
Обозначим nj(x) - средний выигрыш первого в расчете на партию, когда он использует стратегию (х, 1-х), а второй - j-ю стратегию.
Имеем
n1(x)=х - 2(1-х);
n2(x)=2х +(1-х);
n3(x)=-4х + 2(1-х);
n4(x)=3х - 3(1-х).
Возьмем на плоскости систему координат, по горизонтальной оси вправо отложим х, по вертикальной оси - значения функции nj(x). Функции n1(x), n2(x), n3(x), n4(x) - линейные, значит их графики - прямые линии 1, 2, 3, 4 соответственно.
Находим нижнюю огибающую огибающую семейства четырех прямых.
Находим ее высшую точку - М. Она и дает решение игры. Ее координаты определяются решением уравнения n2(x)=n4(x), откуда х*=4/5, n=n2(x)=n4(x)=9/5.
Таким образом, оптимальная стратегия первого есть Р*=(4/5, 1/5), а цена игры n=9/5.
Заметим, что при этой стратегии первого второй игрок не выбирает первый и третий столбцы. Обозначим вероятность выбора вторым игроком второго столбца через y, а четвертого столбца - через (1 - y). Учтем, например, что р1*=х*>0 и воспользуемся утверждением о том, что если рк*>0, то М(1; y*)=n, т.е.
2y* +(1-y*)=9/5, откуда y*=4/5.
Окончательный ответ таков: оптимальная стратегия первого Р*=(4/5, 1/5), оптимальная стратегия второго - Q=(0;4/5;0;1/5), цена игры n=15/11.