Задача по теории игр
Задание. Предприятие рассматривает три стратегии сбыта своей продукции. Продукция может реализовываться на близких к производству рынках сбыта (стратегия A1), может отправляться в крупные мегаполисы страны (стратегия A2), а также возможен экспорт товаров (стратегия A3). Прибыль предприятия зависит от конъюнктуры рынка данных изделий. К моменту начала продаж рынок может оказаться в одном из двух состояний (B1 и B2). Прибыль, которую получает предприятие при каждом варианте сбыта и соответствующем состоянии спроса, определяется матрицей:| B1 | B2 | |
| A1 | 6 | 8 |
| A2 | 12 | 6 |
| A3 | 14 | 6 |
Найти процентное соотношение вариантов сбыта продукции, обеспечивающее среднюю величину прибыли при любом состоянии спроса.
Решение:
| Игроки | B1 | B2 | a = min(Ai) |
| A1 | 6 | 8 | 6 |
| A2 | 12 | 6 | 6 |
| A3 | 14 | 6 | 6 |
| b = max(Bi) | 14 | 8 |
Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(ai) = 6, которая указывает на максимальную чистую стратегию A1.
Верхняя цена игры b = min(bj) = 8.
Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры находится в пределах 6 <= y <= 8. Находим решение игры в смешанных стратегиях. Объясняется это тем, что игроки не могут объявить противнику свои чистые стратегии: им следует скрывать свои действия. Игру можно решить, если позволить игрокам выбирать свои стратегии случайным образом (смешивать чистые стратегии)
Решим задачу геометрическим методом, который включает в себя следующие этапы:
1. В декартовой системе координат по оси абсцисс откладывается отрезок, длина которого равна 1. Левый конец отрезка (точка х = 0) соответствует стратегии B1, правый - стратегии B2 (x = 1). Промежуточные точки х соответствуют вероятностям некоторых смешанных стратегий S1 = (p1,p2).
2. На левой оси ординат откладываются выигрыши стратегии B1. На линии, параллельной оси ординат, из точки 1 откладываются выигрыши стратегии B2.
Решение игры (m x 2) проводим с позиции игрока B, придерживающегося максиминной стратегии. Доминирующихся и дублирующих стратегий ни у одного из игроков нет.
Максиминной оптимальной стратегии игрока B соответствует точка N, лежащая на пересечении прямых A1A1 и A3A3, для которых можно записать следующую систему уравнений:
y = 6 + (8 - 6)q2
y = 14 + (6 - 14)q2
Откуда
q1 = 1/5
q2 = 4/5
Цена игры, y = 73/5
Теперь можно найти минимаксную стратегию игрока A, записав соответствующую систему уравнений, исключив стратегию A2, которая дает явно больший проигрыш игроку A, и, следовательно, p2 = 0.
6p1+14p3 = y
8p1+6p3 = y
p1+p3 = 1
или
6p1+14p3 = 73/5
8p1+6p3 = 73/5
p1+p3 = 1
Решая эту систему методом обратной матрицы, находим:
p1 = 4/5
p3 = 1/5
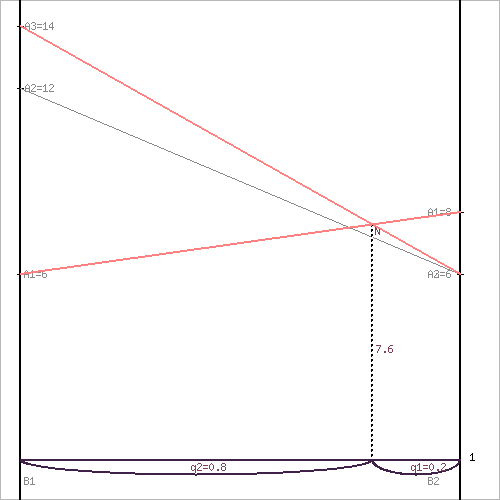
Ответ: Цена игры: y = 73/5, векторы стратегии игроков: P(4/5, 0, 1/5), Q(1/5, 4/5)
Таким образом, для первой стратегии необходимо реализовывать 4/5 от всей продукции, или 80%, для третьей стратегии – 1/5 или 20%.

