Методы упрощения платёжных матриц. Доминирование и дублирование стратегий
Рассмотрим несколько методов упрощения платёжных матриц.Первый метод, используемый для уменьшения размерности матрицы, основан на одном из важнейших понятий в теории игр - понятии доминирования стратегий (мажорирование стратегий).
Если i-я строка поэлементно не меньше (≥) j-й строки, то говорят, что i-я строка доминирует над j-й строкой. Поэтому игрок A не использует j-ю стратегию, так как его выигрыш при i-й стратегии не меньше, чем при j-й стратегии, вне зависимости от того, как играет игрок B.
Аналогично, если i-й столбец поэлементно не меньше (≥) j-го столбца, то говорят, что j-й столбец доминирует над i-м столбцом. Поэтому игрок B не использует i-ю стратегию, так как его проигрыш (равный выигрышу игрока A) при j-й стратегии не больше (≤), чем при i-й стратегии, вне зависимости от того, как играет игрок A. Стратегии, над которыми доминируют другие стратегии, надо отбросить и приписать им нулевые вероятности. На цене игры это никак не скажется. Зато размер матрицы игры понизится. С этого и нужно начинать решение игры.
Частный случай доминирования является дублирование стратегий.
Если платёжная матрица игры содержит несколько одинаковых строк (столбцов), то из них оставляем только одну строку, а остальные строки (столбцы) отбрасываем. Отброшенным стратегиям припишем нулевые вероятности.
Упрощение (уменьшение размерности) платёжных матриц за счёт исключения заведомо невыгодных чистых стратегий возможно в силу справедливости следующей Теоремы о доминирующих стратегиях:
Пусть I - игра, в матрице которой i -я стратегия первого игрока доминирует над i +1, а G - игра, матрица которой получена из матрицы I исключением i + 1 стратегии (строки). Тогда:
- цена игры I равна цене игры G;
- оптимальная смешенная стратегия Q*= (q1*,q2*,…,qn*) второго игрока в игре G является также его оптимальной смешанной стратегией в игре I;
- если P*= (p1*,p2*,…,pi*, p*i+2,…, pm*) оптимальная смешенная стратегия первого игрока в игре G, то его смешенная стратегия P*= (p1*,p2*,…,pi*, p*i+2,…, pm*) является оптимальной в игре I.
Рассмотрим ряд примеров с использованием калькулятора Решение матричной игры
.
Пример 1. Платёжная матрица игры задана в виде:  .
.
1-я и 4-я строки равны. Поэтому отбросим 4-ю строку. Вероятность p4 = 0. Получим матрицу:
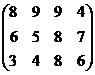 .
. ![]()
2-я строка доминирует над 3-й строкой (6 > 3, 5 > 4, 8 = 8, 7 > 6). Поэтому отбросим 3-ю строку. Вероятность p3 = 0. Получим матрицу:
![]() .
.
2-й столбец доминирует над 3-м столбцом (9 = 9, 5 < 8). Поэтому отбросим 3-й столбец. Вероятность q3 = 0. Получим матрицу:
![]() .
.
Строки между собой не сравнимы (8 > 6, 4 < 7), столбцы тоже (8 < 9, 6 > 5; 8 > 4, 6 < 7; 9 > 4, 5 < 7). Дальнейшее упрощение невозможно. Мы свели игру 4×4 к игре 2×3.
Пример 2. Матрица игры
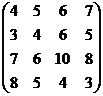 .
.
Упростить игру.
Введём вероятностные векторы: P = (p1, p2, p3, p4), Q = (q1, q2, q3, q4).
1 - ый шаг: A1 доминирует A2: вычёркиваем 2- ю строку, в результате получаем р2= 0 и платёжную матрицу:
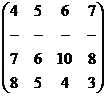
2-ой шаг: A3 доминирует A1: вычёркиваем 1- ю строку, в результате получаем р1= 0 и платёжную матрицу:
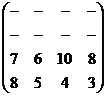
3-ий шаг: B2 доминирует B1 вычёркиваем 1- ый столбец, в результате получаем q1 = 0 и платёжную матрицу:
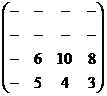
4-ый шаг: B4 доминирует B3 вычёркиваем 2 - ый столбец, в результате получаем q3 = 0 и платёжную матрицу:

5 -ый шаг: A3 доминирует A4: вычёркиваем 4 - ю строку, в результате получаем p4= 0 и платёжную матрицу:

6 - ой шаг: B2 доминирует B4 вычёркиваем 4 - ый столбец, в результате получаем q4 = 0 и платёжную матрицу:

В результате упрощения платёжной матрицы выяснилось, что игра имеете единственное оптимальное решение в чистых стратегиях, о чём говорят векторы вероятностей P и Q:
P = (0, 0, p3, 0), Q = (0, q2, 0, 0).
В результате упрощения платёжной матрицы было установлено также наличие седловой точки и получено оптимальное решение в чистых стратегиях: первый игрок A должен действовать, все время, выбирая стратегию A3, а игрок B выбирает стратегию B2.
Тот же результат получается, если использовать максиминную стратегию.
V* = max min aij = max{4,3,6,3}= 6
V* = min max aij = min{8,6,10,8}= 6
V* = V* = 6, элемент матрицы а32 является седловой точкой.
Замечание. Если игра m×n имеет седловую точку, то после упрощений платёжной матрицы мы всегда получим игру 1×1.
Продолжим рассмотрение методов упрощения платёжной матрицы.
Другой метод преобразования матрицы выигрышей (платёжной матрицы) основывается на доказываемой в теории игр теореме об аффинных преобразованиях.
Теорема об аффинных преобразованиях. Аффинное преобразование (преобразование подобия и сдвига) платежной матрицы, т.е. преобразование всех элементов матрицы A вида: a'ij = k*aij+b, где k ≠ 0 и b - любая константа, не изменяет решение игры. Кроме того, цена преобразованной игры V' может быть получена из цены первоначальной игры V по тому же правилу: V' = kV + b
Это означает, в частности, что для задания игры в принципе безразлично, в каких единицах измеряется выигрыш, например, в рублях или другой валюте.
Прибавление (вычитание) некоторой фиксированной суммы bк каждому из элементов aij платёжной матрицы A изменит на такую же сумму выигрыш (проигрыш) каждого из игроков, не меняя при этом решения игры. Это свойство может быть использовано для преобразования исходной матрицы игры к более удобному виду. Так, например, если элементы платежной матрицы представляют собой дроби с общим знаменателем, то каждый элемент матрицы aij можно умножить на некоторую константу, в результате чего элементы преобразованной матрицы будут представлять собой целые числа; если же большинство клеток матрицы заполнены одинаковыми элементами, то их можно вычесть из каждого элемента матрицы для получения нулей, которым будут равны соответствующие элементы матрицы. Кроме того, цену игры V' всегда можно сделать положительной, т.е. V' > 0, чем мы воспользуемся при сведении игровой задачи к задаче линейного программирования.
В завершении данного параграфа приведём формулу пересчёта от преобразованной цены игры V' к исходной V:
![]()
Пример 3. Задана платёжная матрица игры:
A = 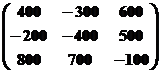
Необходимо упростить матрицу игры.
1 - ый шаг: умножим каждый из элементов матрицы A на k = 0.01, получим:
![]()
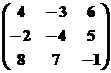
2 - ой шаг: к каждому элементу матрицы A' прибавим b = 4, получим матрицу:
![]() =
= 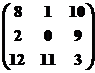
Таким образом, мы получили платёжную матрицу с положительными элементами и небольшими по абсолютной величине. Работа с такой матрицей проще, чем с исходной матрицей. Элементы матрицы A'' получены преобразованием:
Перейти к онлайн решению своей задачи
Пример 4. Платёжная матрица игры задана в виде. Упростить игру (упростить платёжную матрицу) найти оптимальное решение.

