Оптимальные чистые стратегии игроков
Чистой стратегией игрока I является выбор одной из n строк матрицы выигрышей А, а чистой стратегией игрока II является выбор одного из столбцов этой же матрицы.Оптимальные чистые стратегии игроков отличаются от смешанных наличием обязательного единичного pi = 1, qi = 1. Например: P(1,0), Q(1,0). Здесь p1 = 1, q1 = 1.
Задача 1
По платёжной матрице найти оптимальные чистые стратегии, используя принцип строгого доминирования. В качестве ответа записать векторы P*, Q*.
R1 | R2 | R3 | R4 | |
S1 | 3 | 1 | 2 | 5 |
S2 | 2 | 0 | 0 | 3 |
S3 | -3 | -5 | -5 | -2 |
S4 | 0 | -2 | -2 | 1 |
Решение:
Все задачи решаем с помощью калькулятора Матричная игра
.
1. Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях.
Считаем, что игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I.
| Игроки | B1 | B2 | B3 | B4 | a = min(Ai) |
| A1 | 3 | 1 | 2 | 5 | 1 |
| A2 | 2 | 0 | 0 | 3 | 0 |
| A3 | -3 | -5 | -5 | -2 | -5 |
| A4 | 0 | -2 | -2 | 1 | -2 |
| b = max(Bi) | 3 | 1 | 2 | 5 |
Верхняя цена игры b = min(bj) = 1.
Седловая точка (1, 2) указывает решение на пару альтернатив (A1,B2). Цена игры равна 1.
2. Проверяем платежную матрицу на доминирующие строки и доминирующие столбцы.
Иногда на основании простого рассмотрения матрицы игры можно сказать, что некоторые чистые стратегии могут войти в оптимальную смешанную стратегию лишь с нулевой вероятностью.
Говорят, что i-я стратегия 1-го игрока доминирует его k-ю стратегию, если aij ≥ akj для всех j Э N и хотя бы для одного j aij > akj. В этом случае говорят также, что i-я стратегия (или строка) – доминирующая, k-я – доминируемая.
Говорят, что j-я стратегия 2-го игрока доминирует его l-ю стратегию, если для всех j Э M aij ≤ ail и хотя бы для одного i aij < ail. В этом случае j-ю стратегию (столбец) называют доминирующей, l-ю – доминируемой.
Стратегия A1 доминирует над стратегией A2 (все элементы строки 1 больше или равны значениям 2-ой строки), следовательно исключаем 2-ую строку матрицы. Вероятность p2 = 0.
Стратегия A1 доминирует над стратегией A3 (все элементы строки 1 больше или равны значениям 3-ой строки), следовательно исключаем 3-ую строку матрицы. Вероятность p3 = 0.
| 3 | 1 | 2 | 5 |
| 0 | -2 | -2 | 1 |
С позиции проигрышей игрока В стратегия B1 доминирует над стратегией B2 (все элементы столбца 1 больше элементов столбца 2), следовательно исключаем 1-й столбец матрицы. Вероятность q1 = 0.
С позиции проигрышей игрока В стратегия B4 доминирует над стратегией B1 (все элементы столбца 4 больше элементов столбца 1), следовательно исключаем 4-й столбец матрицы. Вероятность q4 = 0.
| 1 | 2 |
| -2 | -2 |
Мы свели игру 4 x 4 к игре 2 x 2.
3. Находим решение игры в смешанных стратегиях.
Решим задачу геометрическим методом, который включает в себя следующие этапы:
1. В декартовой системе координат по оси абсцисс откладывается отрезок, длина которого равна 1. Левый конец отрезка (точка х = 0) соответствует стратегии A1, правый - стратегии A2 (x = 1). Промежуточные точки х соответствуют вероятностям некоторых смешанных стратегий S1 = (p1,p2).
2. На левой оси ординат откладываются выигрыши стратегии A1. На линии, параллельной оси ординат, из точки 1 откладываются выигрыши стратегии A2.
Решение игры (2 x n) проводим с позиции игрока A, придерживающегося максиминной стратегии. Доминирующихся и дублирующих стратегий ни у одного из игроков нет.
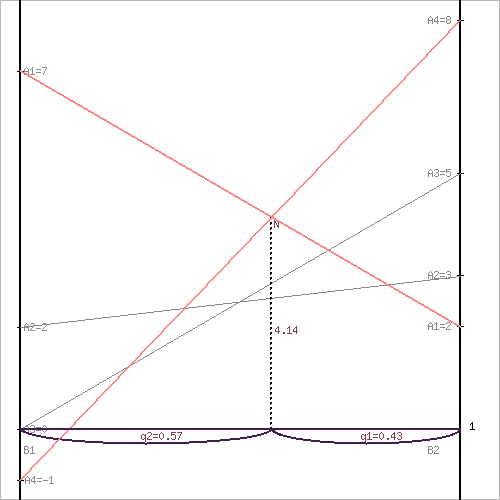
Максиминной оптимальной стратегии игрока A соответствует точка N, для которой можно записать следующую систему уравнений:
p1 = 1
p2 = 0
Цена игры, y = 1
Теперь можно найти минимаксную стратегию игрока B, записав соответствующую систему уравнений
q1 = 1
q1+q2 = 1
Решая эту систему, находим:
q1 = 1.
Ответ:
Цена игры: y = 1, векторы стратегии игроков:
Q(1, 0), P(1, 0)
4. Проверим правильность решения игры с помощью критерия оптимальности стратегии.
∑aijqj ≤ v
∑aijpi ≥ v
M(P1;Q) = (1•1) + (2•0) = 1 = v
M(P2;Q) = (-2•1) + (-2•0) = -2 ≤ v
M(P;Q1) = (1•1) + (-2•0) = 1 = v
M(P;Q2) = (2•1) + (-2•0) = 2 ≥ v
Все неравенства выполняются как равенства или строгие неравенства, следовательно, решение игры найдено верно.
Поскольку из исходной матрицы были удалены строки и столбцы, то найденные векторы вероятности можно записать в виде:
P(1,0,0,0)
Q(0,1,0,0)
Задача 2
По платёжной матрице найти нижнюю и верхнюю цену игры. При наличии седловой точки записать векторы оптимальных чистых стратегий P*, Q*.
R1 | R2 | R3 | |
S1 | -6 | -5 | 0 |
S2 | -8 | -3 | -2 |
S3 | -3 | -2 | 3 |
Решение:
1. Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях.
Считаем, что игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I.
| Игроки | B1 | B2 | B3 | a = min(Ai) |
| A1 | -6 | -5 | 0 | -6 |
| A2 | -8 | -3 | -2 | -8 |
| A3 | -3 | -2 | 3 | -3 |
| b = max(Bi) | -3 | -2 | 3 |
Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(ai) = -3, которая указывает на максимальную чистую стратегию A3.
Верхняя цена игры b = min(bj) = -3.
Седловая точка (3, 1) указывает решение на пару альтернатив (A3,B1). Цена игры равна -3.
Ответ: P(0,0,1), Q(1,0,0)
Задача 3
По платёжной матрице найти векторы оптимальных стратегий P*, Q*и цену игры. Кто из игроков оказывается в выигрыше?
R1 | R2 | R3 | R4 | |
S1 | -6 | -6 | 2 | 4 |
S2 | 2 | -2 | 7 | -1 |
Решение:
1. Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях.
Считаем, что игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I.
| Игроки | B1 | B2 | B3 | B4 | a = min(Ai) |
| A1 | -6 | -6 | 2 | 4 | -6 |
| A2 | 2 | -2 | 7 | -1 | -2 |
| b = max(Bi) | 2 | -2 | 7 | 4 |
Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(ai) = -2, которая указывает на максимальную чистую стратегию A2.
Верхняя цена игры b = min(bj) = -2.
Седловая точка (2, 2) указывает решение на пару альтернатив (A2,B2). Цена игры равна -2.
3. Находим решение игры в смешанных стратегиях.
Решим задачу геометрическим методом, который включает в себя следующие этапы:
1. В декартовой системе координат по оси абсцисс откладывается отрезок, длина которого равна 1. Левый конец отрезка (точка х = 0) соответствует стратегии A1, правый - стратегии A2 (x = 1). Промежуточные точки х соответствуют вероятностям некоторых смешанных стратегий S1 = (p1,p2).
2. На левой оси ординат откладываются выигрыши стратегии A1. На линии, параллельной оси ординат, из точки 1 откладываются выигрыши стратегии A2.
Решение игры (2 x n) проводим с позиции игрока A, придерживающегося максиминной стратегии. Доминирующихся и дублирующих стратегий ни у одного из игроков нет.
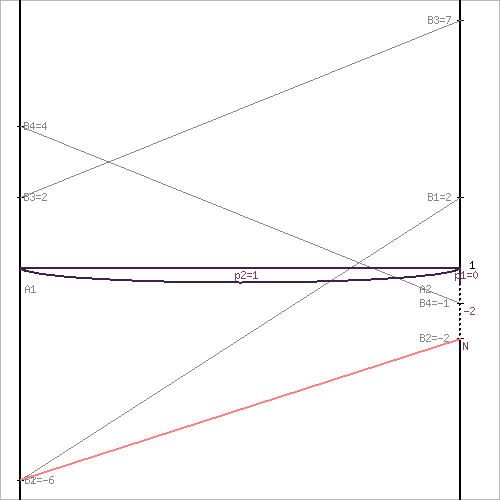
p1 = 0
p2 = 1
Цена игры, y = -2
Теперь можно найти минимаксную стратегию игрока B, записав соответствующую систему уравнений, исключив стратегию B1,B3,B4, которая дает явно больший проигрыш игроку B, и, следовательно, q1 = 0,q3 = 0,q4 = 0.
-2q2 = -2
q2 = 1
Решая эту систему, находим:
q2 = 1.
Ответ:
Цена игры: y = -2, векторы стратегии игроков:
Q(0, 1, 0, 0), P(0, 1)
4. Проверим правильность решения игры с помощью критерия оптимальности стратегии.
∑aijqj ≤ v
∑aijpi ≥ v
M(P1;Q) = (-6•0) + (-6•1) + (2•0) + (4•0) = -6 ≤ v
M(P2;Q) = (2•0) + (-2•1) + (7•0) + (-1•0) = -2 = v
M(P;Q1) = (-6•0) + (2•1) = 2 ≥ v
M(P;Q2) = (-6•0) + (-2•1) = -2 = v
M(P;Q3) = (2•0) + (7•1) = 7 ≥ v
M(P;Q4) = (4•0) + (-1•1) = -1 ≥ v
Все неравенства выполняются как равенства или строгие неравенства, следовательно, решение игры найдено верно.
Задача 4
Дайте развернутый ответ на вопрос
Что такое верхняя цена игры?
Поясните на примере любой из предыдущих задач.

