Приведение матричной антагонистической игры к задачам линейного программирования
В данном статье описано сведение матричной игры к задаче линейного программирования.Алгоритм поиска решения матричной антагонистической игры, заданной платежной матрицей, имеющей размерность m×n при больших значениях m и n, сводится к алгоритму симплекс-метода решения пары взаимодвойственных задач линейного программирования. Покажем, как привести конечную матричную антагонистическую игру к двум взаимодвойственных задачам линейного программирования.
Пусть антагонистическая игра задана платёжной матрицей A, имеющей размерность m×n, и эта игра является не вполне определённой. Необходимо найти решение игры, т.е. определить оптимальные смешанные стратегии первого и второго игроков:
P*= (p1*, p2*, …, pm*), Q*= (q1*, q2*,…, qn*)
где P* и Q* - векторы, компоненты которых pi* и pj* характеризуют вероятности применения чистых стратегий i и j соответственно первым и вторым игроками и соответственно для них выполняются соотношения:
p1* + p2* + … + pm* = 1, q1* + q2* + … + qn* = 1
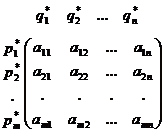
Найдём сначала оптимальную стратегию первого игрока P*. Эта стратегия должна обеспечить выигрыш первому игроку не меньше V, т.е. ≥V , при любом поведении второго игрока, и выигрыш, равный V , при его оптимальном поведении, т.е. при стратегии Q*.
Цена игры V нам пока неизвестна. Без ограничения общности, можно предположить её равной некоторому положительному числу V>0. Действительно, для того, чтобы выполнялось условие V > 0, достаточно, чтобы все элементы матрицы A были неотрицательными. Этого всегда можно добиться с помощью аффинных преобразований: прибавляя ко всем элементам матрицы A одну и ту же достаточно большую положительную константу М; при этом цена игры увеличится на М, а решение не изменится. Итак, будем считать V > 0.
Предположим, что первый игрок A применяет свою оптимальную стратегию P*, а второй игрок B свою чистую стратегию j -ю, тогда средний выигрыш (математическое ожидание) первого игрока A будет равен:
Оптимальная стратегия первого игрока (A ) обладает тем свойством, что при любом поведении второго игрока (B) обеспечивает выигрыш первому игроку, не меньший, чем цена игры V; значит, любое из чисел aj не может быть меньше V (≥ V). Следовательно, при оптимальной стратегии, должна выполняться следующая система неравенств:
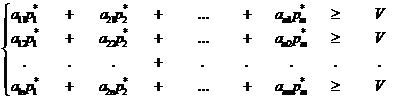(1)
Разделим неравенства (1) на положительную величину V (правые части системы (1)) и введём обозначения:
(2)
y1 ≥ 0, y2 ≥ 0, .., ym ≥ 0, (3)
Тогда условия (1) запишутся в виде:
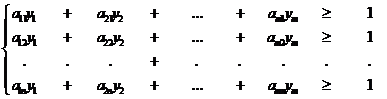(4)
где y1,y2,...ym - неотрицательные переменные. В силу (2) и того, что p1* + p2* + … + pm* = 1 переменные y1, y2 , ..., ym удовлетворяют условию, которое обозначим через F:
(5)
Поскольку первый игрок свой гарантированный выигрыш (V) старается сделать максимально возможным (V→ max) , очевидно, при этом правая часть (5) -
→min - принимает минимальное значение. Таким образом, задача решения антагонистической игры для первого игрока свелась к следующей математической задаче:
определить неотрицательные значения переменных y1, 2, ... , yn, чтобы они удовлетворяли системе функциональных линейных ограничений в виде неравенств (4), системе общих ограничений (3) и минимизировали целевую функцию F:
F = y1 + y2 + ... + ym→ min
Это типичная задача линейного программирования (двойственная) и она может быть решена симплекс - методом. Таким образом, решая задачу линейного программирования, мы можем найти оптимальную стратегию P*= (p1*, p2*, …, pm*) игрока A.
Найдём теперь оптимальную стратегию Q*= (q1*, q2*,…, qn*)
игрока B. Всё будет аналогично решению игры для игрока A, с той разницей, что игрок B стремиться не максимизировать, а минимизировать выигрыш (по сути дела его проигрыш), а значит, не минимизировать, а максимизировать величину , т.к. V →min. Вместо условий (4) должны выполняться условия:
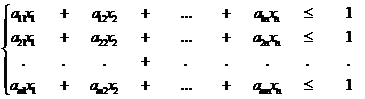(6)
где
(7)
x1 ≥ 0, x2 ≥ 0, .., xn ≥ 0 (8)
Требуется так выбрать переменные x1, x2, .., xn, чтобы они удовлетворяли условиям (6), (8) и обращали в максимум линейную функцию цели F/:
Таким образом, задача решения антагонистической игры для второго игрока свелась к следующей математической задаче:
определить неотрицательные значения переменных x1, x2, .., xn, чтобы они удовлетворяли системе функциональных линейных ограничений в виде неравенств (6), системе общих ограничений (8) и максимизировать целевую функцию F/:
F' = x1 + x2 + .. + xn → min
Это типичная задача линейного программирования (прямая) и она может быть решена симплекс - методом. Таким образом, решая прямую задачу линейного программирования, мы можем найти оптимальную стратегию Q*= (q1*, q2*,…, qn*) игрока B.
Подведём итог.
| Задача второго игрока минимизация проигрыша V | Задача первого игрока максимизация выигрыша V |
| Целевая функция | |
F/= x1+x2+x3+....+xn= → max |
F = y1+y2+y3+...+ym= → min |
| Функциональные ограничения | |
 |
 |
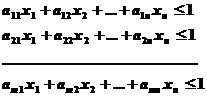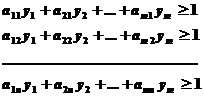| Общие (прямые) ограничения | |
| x1 ≥ 0, x2 ≥ 0, .., xn≥ 0 | y1 ≥ 0, y2 ≥ 0, .., ym≥ 0 |
Примечание
Из сведения задачи решения конечной матричной антагонистической игры к задаче линейного программирования (ЗЛП) можно сделать заключение по поводу существования решения антагонистической игры m × n, не опираясь на теорему фон Неймана.
Пусть задача о нахождении оптимальной стратегии P*= (p1*, p2*, …, pm*) игрока A сведена к задаче линейного программирования с условиями неравенствами (4) и минимизируемой функцией (5). Всегда ли существует её решение? Известно, что решение задачи линейного программирования может и не существовать; оно отсутствует, если:
1. функциональные и общие условия - равенства или неравенства - вообще не имеют допустимых неотрицательных решений;
2. допустимые решения существуют, но среди них нет оптимального, так как минимизируемая функция не ограничена снизу.
Все преобразования можно получить через онлайн-калькулятор
Решение матричной игры
Посмотрим, как обстоит дело в нашем случае. Допустимые решения ЗЛП в нашем случае всегда существуют. Действительно, с помощью аффинных преобразований сделаем элементы платёжной матрицы A строго положительными, например, прибавив достаточно большое положительное число М к каждому элементу платёжной матрицы, и обозначим наименьший элемент матрицы A через μ:
μ = min min aij
i j
Положим теперь y1 = 1/μ, y2 = y3 = ... = ym
= 0. Нетрудно видеть, что эта система значений переменных х1, х2 , х3,..., хm
представляют собой допустимое решение ЗЛП - все они неотрицательны, и их совокупность удовлетворяет условиям (4).
Теперь убедимся, что линейная функция (5) не может быть неограниченной снизу. Действительно, все y1, y2 , y3,..., ym неотрицательны, а коэффициенты при них в в выражении (5) положительные (равные единицам), значит, функция F в формуле (5) тоже неотрицательна, значит, она ограничена снизу (нулём) и решение задачи линейного программирования (а следовательно, и игры m × n) существует.
Перейти к онлайн решению своей задачи
Пример 1. Решить игру с матрицей:
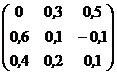
1. В соответствии с алгоритмом определим, существуют ли в ней доминируемые стратегии, чтобы исключить их. Доминируемых стратегий нет.
2. Поскольку матрица содержит отрицательные числа, то нужно добиться, чтобы все её элементы были неотрицательны, прибавив ко всем её элементам число, равное модулю наименьшего числа матрицы. Минимальный элемент матрицы равен - 0,1, его модуль равен 0,1. Прибавим ко всем элементам платёжной матрицы число, равное 0,1 , в результате получим:
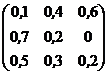
Умножим все элементы полученной матрицы на 10, чтобы удобнее проводить последующие вычисления.
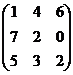
Проведённые аффинные преобразования на оптимальных стратегиях не скажутся, а цену игры мы восстановим, сделав обратные преобразования (разделим полученную сумму на 10 и отнимем 0,1).
Припишем строкам вероятности p1, p2, p3.
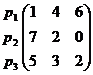
Тогда среднее значение (математическое ожидание) выигрыша игрока A при применении игроком B своей первой стратегии равен 1·p1 + 7·p2 + 5·p3 (первый столбец поэлементно умножаем на вероятности p1, p2, p3 и полученные произведения суммируем). Это выигрыш не может быть меньше гарантированной цены игры V: 1·p1 + 7·p2 + 5·p3 ≥ V. Аналогично для других стратегий игрока B.
p1+7p2+5p3≥V
4p1+2p2+3p3≥V
6p1+2p3≥V
pi≥0, i=1,2,3
Разделим обе части неравенства на V и введём обозначения yi = pi/V (i=1,2,3.):
y1+7y2+5y3≥1
4y1+2y2+3y3≥1
6y1+2y3≥1
yi≥0, i=1,2,3
Игрок A стремиться повысить цену игры (V→ max). Поэтому F→ min.
Получили задачу линейного программирования:
F = y1 + y2 + y3 → min
y1+7y2+5y3≥1
4y1+2y2+3y3≥1
6y1+2y3≥1
yi≥0, i=1,2,3
Аналогично припишем столбцам вероятности q1, q2, q3.
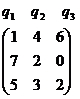
Тогда средний проигрыш игрока B при применении игроком A его первой стратегии равен 1·q1 + 4·q2 + 6·q3 (1-ю строку поэлементно умножаем на вероятности q1,q2, q3 и полученные произведения суммируем). Этот проигрыш не может быть больше цены игры V: 1·q1 + 4·q2 + 6·q3 ≤ V. Аналогично для других стратегий игрока A.
q1+4q2+6q3≤V
7q1+2q2≤V
5q1+3q2+2q3≤V
qi≥0, i=1,2,3
Разделим обе части неравенств на V и введём обозначения xi = qi /V (i = 1, 2, 3)
x1+4x2+6x3≤1
7x1+2x2≤1
5x1+3x2+2x3≤1
xi≥0, i=1,2,3
Игрок B стремится понизить цену игры (V→min), поэтому F/ → max.
Получили задачу линейного программирования:
F' = x1 + x2 + x3 → max
x1+4x2+6x3≤1
7x1+2x2≤1
5x1+3x2+2x3≤1
xi≥0, i=1,2,3
Полученные задачи являются взаимно двойственными задачами линейного программирования. Решим любую из них симплекс-методом. Окончательный результат - таблица имеет следующий вид:
| у1 | 3/28 | p1= | 3/8 | |
| у2 | 0 | p2= | 0 | |
| у3 | 5/28 | p3= | 5/8 | |
| F/ | 2/7 | V= | 3 1/2 |
| х1 | 1/7 | q1= | 1/2 | |
| х2 | 0 | q2= | 0 | |
| х3 | 1/7 | q3= | 1/2 | |
| F | 2/7 | V= | 3 1/2 |
Итак, оптимальные стратегии:
Р*=(3/8; 0; 5/8), Q*=(1/2; 0; 1/2),
цена игры:
для модифицированной задачи V= 3.5, а для исходной задачи V/ = 3.5/10-0.1 = 0.25.
