Решение задачи линейного программирования графически в трехмерном пространстве
Если в задаче три переменные, то она тоже допускает графическое решение в трехмерном пространстве. При этом рисунок делается условный, не строго выдерживая масштаб. Однако взаимное расположение точек на осях должно быть верным и соответствующим их числовым значениям.Решить задачу линейного программирования двумя методами: графически в трехмерном пространстве и симплекс-методом.
f = 2x + 5y + 2z → max
при условиях x+4y+4z ≤ 16, 3x+2y+4z ≤ 20, x,y,z ≥ 0
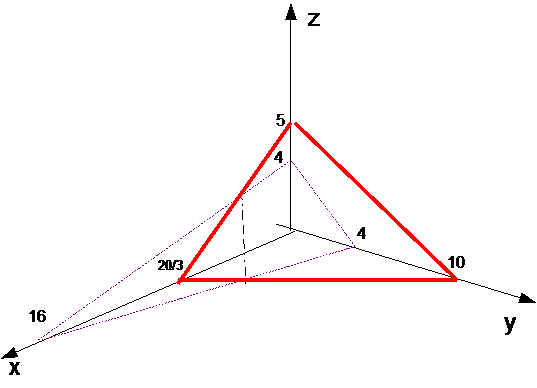
Находится линия пересечения этих треугольников. Точнее, находятся координаты двух точек, являющихся концами части этой линии пересечения, лежащей в первом октанте. Множество допустимых планов (как правило) является симплексом с конечным числом угловых точек. Все эти угловые точки указывают на рисунке и точно вычисляют их координаты.
x+4y+4z = 16
3x+2y+4z = 20
1) при z = 0
x+4y = 16
3x+2y = 20
-5x = -24, откуда x = 4,8; y = 2,8; z = 0
2) y = 0
x+4z = 16
3x+4z = 20
2x = 4, откуда x = 2, y = 0, z = 3
Потом вычисляют значение целевой функции во всех угловых точках и выбирают из них оптимальное.
F(4,8; 2,8; 0) = 2*4,8 + 5*2,8 + 2*0 = 23,6
F(2; 0; 3) = 2*2+ 5*0 + 2*3 = 10
Ответ: x = 4,8; y = 2,8; z = 0, fmax = 23,6
Пример №1. Решить задачу линейного программирования графически в трехмерном пространстве.
f(x) = 3x1 + 5x2 – x3
при ограничениях
x1 + x2 + 2x3 = 6
x2 + x3 – x4 = 4
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
Решение. Проведем анализ задачи. В задаче 4 переменные и 2 основных ограничения в виде равенств (не считая условия неотрицательности). Так как ограничения даны в виде равенств, то задача в канонической форме. В данном виде геометрически задачу не решить, так как много переменных.
Решим задачу графически, преобразовав каноническую форму задачи линейного программирования к стандартному виду. У нас два ограничения и есть две переменные, каждая из которых встречается только в одном уравнении. Эти переменные можно исключить из задачи, тем самым упростив её формулировку. Исключаемыми переменными объявим первую и последнюю.
Для этого из первого условия системы ограничений выразим x1 = 6- x2 - 2x3 , а из второго уравнения x4 = x2 + x3 - 4.
Подставим x1 = 6- x2 - 2x3 в целевую функцию и получим новую целевую функцию
F = 18 + 2x2 – 7x3 и новую систему ограничений без переменных x1, x4:
x2 + 2x3 ≤6
x2 + x3 ≥ 4
x2 ≥ 0, x3 ≥ 0
За счет неотрицательности исключаемых переменных получили неравенства в разные стороны.
Полученную задачу линейного программирования стандартного вида на плоскости решим графически. На плоскости x2Ox3 изобразим множество допустимых планов, которое удовлетворяет системе ограничений. Получим треугольник с вершинами в точках B(4,0), C(6,0), A(2,2).
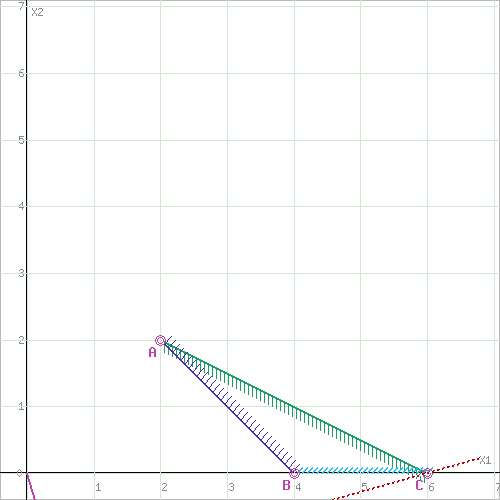
Вычислим значение новой целевой функции в этих угловых точках:
F(B) = F(4,0) = 18 + 8 = 26
F(C) = F(6,0) = 18 + 12 = 30
F(A)= F(2,2) = 18 + 4 – 14 = 8
Получили решение вспомогательной (новой) задачи: x2 = 6, x3 = 0, F = 30.
Отсюда вычисляем оптимальный план и максимум исходной задачи:
x1 = 6 – 6 - 0 = 0, x4 = 6 + 0 – 4 = 2, f = F = 30
Ответ. x1 = 0, x2 = 6, x3 = 0, x4 = 2, fmax = 30.
Для решения этой задачи также можно использовать калькулятор.
Пример №2. Найти графическим методом или симплекс-методом какое-нибудь решение системы.
x + y + z = 10
5x +2y +z ≥ 26
6x + 5y + 3z ≤ 57
Решение.
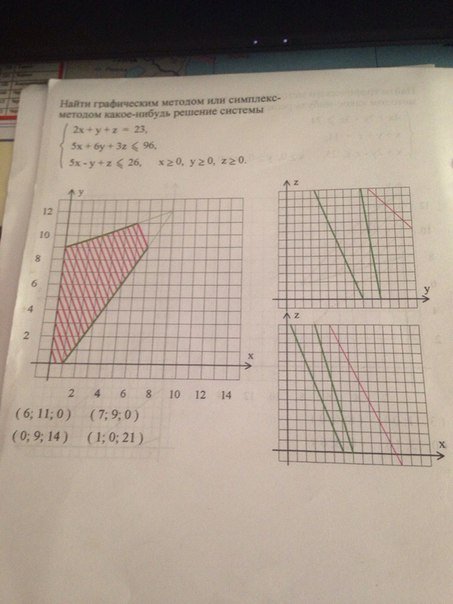
Здесь не задана целевая функция. Однако графическим методом можно найти область допустимых значений (ОДР). Для этого выразить z=10-x-y и подставить в другие уравнения:
5x+2y+10-x-y ≥ 26
6x+5y+30-3x-3y ≤ 57
или
4x+y ≥ 16
3x+2y ≤ 27
Таким образом, осталось две переменные.

