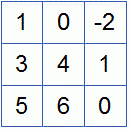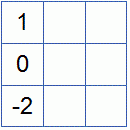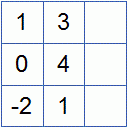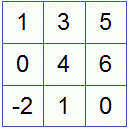
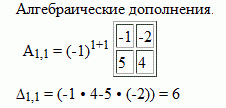Деление многочленов столбиком
Для любых многочленов f(x) и g(x), g(x) ≠ 0, существуют единственные полиномы q(x) и r(x), такие что
f(x)
g(x)
= q(x)+
r(x)
g(x)
Алгоритм деления в столбик применяется в частности при нахождении интегралов.
Пример деления в столбик. Найти частное деления и остаток многочлена:
№1.
| x3 -12x2-42 | x -3 |
| x3 -3x2 | x2 |
| -9x2-42 |
№2.
| x3 -12x2-42 | x -3 |
| x3 -3x2 | x2 -9x |
| -9x2-42 | |
| -9x2 + 27x | |
| -27x -42 |
№3.
| x3 -12x2-42 | x -3 |
| x3 -3x2 | x2 -9x -27 |
| -9x2-42 | |
| -9x2 + 27x | |
| -27x -42 | |
| -27x + 81 | |
| -123 |
Целая часть: x2 -9x -27
Остаток: -123
Таким образом, ответ можно записать как: 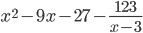
см. также и другие примеры решение столбиком.
Пример №1. Найти частное и остаток от деления многочлена на многочлен:
P(x)=2x5+3x3-x2+4x+1, Q(x)=2x2-x+1
Пример №2. Не производя деление найти остаток от деления многочлена на двучлен:
P(x)=-x4+6x3-2x2+x-2, Q(x)=x-6
Решение. Выделим общий множитель (x-6).
-x3(x-6)-2x(x-6)-12x+x-2 = -x3(x-6)-2x(x-6)-11(x-6)-66-2 = -x3(x-6)-2x(x-6)-11(x-6)-68
Остаток от деления: -68/(x-6)