Назначение сервиса. С помощью данного сервиса в онлайн режиме можно найти алгебраические дополнения, транспонированную матрицу AT, союзную матрицу и обратную матрицу. Решение проводится непосредственно на сайте (в онлайн режиме) и является бесплатным. Результаты вычислений оформляются в отчете формата Word и в формате Excel (т.е. имеется возможность проверить решение). см. пример оформления.
Инструкция. Для получения решения необходимо задать размерность матрицы. Далее в новом диалоговом окне заполните матрицу A.
Нахождение обратной матрицы
Матрица А-1 называется обратной матрицей по отношению к матрице А, если А*А-1 = Е, где Е — единичная матрица n-го порядка. Обратная матрица может существовать только для квадратных матриц.см. также Обратная матрица методом Жордано-Гаусса
Алгоритм нахождения обратной матрицы
- Определяют, квадратная ли матрица. Если нет, то обратной матрицы для нее не существует.
- Вычисление определителя матрицы A. Если он не равен нулю, продолжаем решение, иначе - обратной матрицы не существует.
- Нахождение транспонированной матрицы AT.
- Определение алгебраических дополнений. Заменяют каждый элемент матрицы его алгебраическим дополнением.
- Составление обратной матрицы из алгебраических дополнений: каждый элемент полученной матрицы делят на определитель исходной матрицы. Результирующая матрица является обратной для исходной матрицы.
- Делают проверку: перемножают исходную и полученную матрицы. В результате должна получиться единичная матрица.
- Определяют, квадратная ли матрица. Если нет, то обратной матрицы для нее не существует.
- Вычисление определителя матрицы A. Если он не равен нулю, продолжаем решение, иначе - обратной матрицы не существует.
- Определение алгебраических дополнений.
- Заполнение союзной (взаимной, присоединённой) матрицы C.
- Составление обратной матрицы из алгебраических дополнений: каждый элемент присоединённой матрицы C делят на определитель исходной матрицы. Результирующая матрица является обратной для исходной матрицы.
- Делают проверку: перемножают исходную и полученную матрицы. В результате должна получиться единичная матрица.
Пример №1. Запишем матрицу в виде:
|
∆ = -1·(-1·4-(-2·5))-2·(2·4-(-2·(-2)))+3·(2·5-(-1·(-2))) = 10. Определитель равен 10 и не равен нулю. Продолжаем решение.
Найдем транспонированную матрицу:
| AT = |
|
| A1,1 = (-1)1+1 |
|
| A1,2 = (-1)1+2 |
|
| A1,3 = (-1)1+3 |
|
| A2,1 = (-1)2+1 |
|
| A2,2 = (-1)2+2 |
|
| A2,3 = (-1)2+3 |
|
| A3,1 = (-1)3+1 |
|
| A3,2 = (-1)3+2 |
|
| A3,3 = (-1)3+3 |
|
Тогда обратную матрицу можно записать как:
| A-1 = 1/10 |
|
| A-1 = |
|
Другой алгоритм нахождения обратной матрицы
Приведем другую схему нахождения обратной матрицы.- Находим определитель данной квадратной матрицы A.
- Находим алгебраические дополнения ко всем элементам матрицы A.
- Записываем алгебраические дополнения элементов строк в столбцы (транспонирование).
- Делим каждый элемент полученной матрицы на определитель матрицы A.
Как видим, операция транспонирования может применяться как в начале, над исходной матрицей, так и в конце, над полученными алгебраическими дополнениями.
Особый случай: Обратной, по отношению к единичной матрице E, является единичная матрица E.
Пример №2. Найти матрицу, обратную матрице 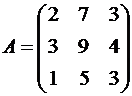 .
.
Решение.
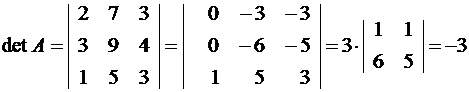 .
.2. Ищем алгебраические дополнения каждого элемента матрицы A:
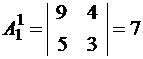 ;
;
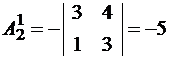 ;
;
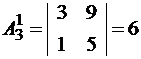 .
.
Получили алгебраические дополнения элементов первой строки. Аналогично для элементов второй и третьей строк получаем:
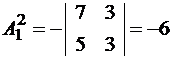 ;
;
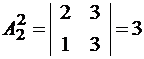 ;
;
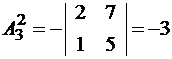 .
.
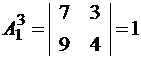 ;
;
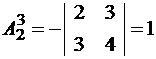 ;
;
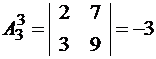 .
.
Объединяя 3 и 4 пункты, получаем обратную матрицу
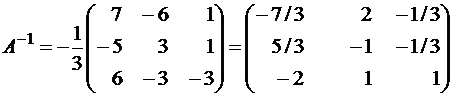 .
.
Для проверки убедимся, что A-1A = E.