Пример нахождения союзной матрицы
Назначение сервиса. С помощью онлайн калькулятора осуществляется расчет союзной матрицы. Результаты вычислений оформляются в отчете формата Word.
Инструкция. Для получения решения необходимо задать размерность матрицы. Далее в новом диалоговом окне заполните матрицу A.
Пример №1. Запишем матрицу в виде:
Главный определитель
∆=2•(9•2-0•8)-(-1•(6•2-0•5))+8•(6•8-9•5)=72
Определитель отличен от нуля, следовательно матрица является невырожденной и для нее можно найти обратную матрицу A-1.
Обратная матрица будет иметь следующий вид:
 | | A11 | A21 | A31 | | A12 | A22 | A32 | | A13 | A23 | A33 |
| |
|
где Aij - алгебраические дополнения.
∆1,1=(9•2-0•8)=18
∆1,2=-(-1•2-8•8)=66
∆1,3=(-1•0-8•9)=-72
∆2,1=-(6•2-0•5)=-12
∆2,2=(2•2-8•5)=-36
∆2,3=-(2•0-8•6)=48
∆3,1=(6•8-9•5)=3
∆3,2=-(2•8-(-1•5))=-21
∆3,3=(2•9-(-1•6))=24
Союзная матрица (взаимная, присоединённая).
Обратная матрица.
| A-1= | | 0,25 | -0,167 | 0,0417 | | 0,917 | -0,5 | -0,292 | | -1 | 0,667 | 0,333 |
| |
|
Проверим правильность нахождения обратной матрицы путем умножения исходной матрицы на обратную. Должны получить единичную матрицу E.
| E=A*A-1= | | 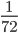 | |
E=A*A-1=| (2•18)+(6•66)+(5•(-72)) | (2•(-12))+(6•(-36))+(5•48) | (2•3)+(6•(-21))+(5•24) |
| (-1•18)+(9•66)+(8•(-72)) | (-1•(-12))+(9•(-36))+(8•48) | (-1•3)+(9•(-21))+(8•24) |
| (8•18)+(0•66)+(2•(-72)) | (8•(-12))+(0•(-36))+(2•48) | (8•3)+(0•(-21))+(2•24) |
Пример №2. Найти обратную матрицу 
Решение.
Главный определитель
∆ = 7∙(6∙3-1∙1)-(-2∙(-2∙3-1∙0.5))+1.5∙(-2∙1-6∙0.5)= 98.5
Транспонированная матрица

Алгебраические дополнения
 ∆1,1 = (6∙3-1∙1) = 17
∆1,1 = (6∙3-1∙1) = 17
 ∆1,2 = -(-2∙3-0.5∙1) = 6.5
∆1,2 = -(-2∙3-0.5∙1) = 6.5
 ∆1,3 = (-2∙1-0.5∙6) = -5
∆1,3 = (-2∙1-0.5∙6) = -5
 ∆2,1 = -(-2∙3-1∙1.5) = 7.5
∆2,1 = -(-2∙3-1∙1.5) = 7.5
 ∆2,2 = (7∙3-0.5∙1.5) = 20.25
∆2,2 = (7∙3-0.5∙1.5) = 20.25
 ∆2,3 = -(7∙1-0.5∙(-2)) = -8
∆2,3 = -(7∙1-0.5∙(-2)) = -8
 ∆3,1 = (-2∙1-6∙1.5) = -11
∆3,1 = (-2∙1-6∙1.5) = -11
 ∆3,2 = -(7∙1-(-2∙1.5)) = -10
∆3,2 = -(7∙1-(-2∙1.5)) = -10
 ∆3,3 = (7∙6-(-2∙(-2))) = 38
∆3,3 = (7∙6-(-2∙(-2))) = 38
Обратная матрица




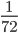

∆1,1 = (6∙3-1∙1) = 17
∆1,2 = -(-2∙3-0.5∙1) = 6.5
∆1,3 = (-2∙1-0.5∙6) = -5
∆2,1 = -(-2∙3-1∙1.5) = 7.5
∆2,2 = (7∙3-0.5∙1.5) = 20.25
∆2,3 = -(7∙1-0.5∙(-2)) = -8
∆3,1 = (-2∙1-6∙1.5) = -11
∆3,2 = -(7∙1-(-2∙1.5)) = -10
∆3,3 = (7∙6-(-2∙(-2))) = 38


