Решение систем линейных неравенств графически
см. также Решение задачи линейного программирования графически, Каноническая форма задач линейного программированияСистема ограничений такой задачи состоит из неравенств от двух переменных:
и целевая функция имеет вид F = C 1 x + C2y, которую необходимо максимизировать.
Ответим на вопрос: какие пары чисел ( x; y ) являются решениями системы неравенств, т. е. удовлетворяют каждому из неравенств одновременно? Другими словами, что значит решить систему графически?
Предварительно необходимо понять, что является решением одного линейного неравенства с двумя неизвестными.
Решить линейное неравенство с двумя неизвестными – это значит определить все пары значений неизвестных, при которых неравенство выполняется.
Например, неравенству 3x
– 5 y ≥ 42 удовлетворяют пары (x , y) : (100, 2); (3, –10) и т. д. Задача состоит в нахождении всех таких пар.
Рассмотрим два неравенства: ax + by≤ c, ax + by≥ c. Прямая ax + by = c делит плоскость на две полуплоскости так, что координаты точек одной из них удовлетворяют неравенству ax + by >c , а другой неравенству ax + +by <c.
Действительно, возьмем точку с координатой x = x 0; тогда точка, лежащая на прямой и имеющая абсциссу x0, имеет ординату
Итак,
Пусть для определенности a< 0, b>0,
c >0. Все точки с абсциссой x0, лежащие выше P (например, точка М), имеют yM>y0, а все точки, лежащие ниже точки P, с абсциссой x0, имеют yN<y0.
Поскольку x0 –произвольная точка, то всегда с одной стороны от прямой будут находиться точки,
для которых ax+ by > c, образующие полуплоскость, а с другой стороны – точки, для которых ax + by< c.
Рисунок 1
Знак неравенства в полуплоскости зависит от чисел a, b , c.
Отсюда вытекает следующий способ графического решения систем линейных неравенств от двух переменных. Для решения системы необходимо:
- Для каждого неравенства выписать уравнение, соответствующее данному неравенству.
- Построить прямые, являющиеся графиками функций, задаваемых уравнениями.
- Для каждой прямой определить полуплоскость, которая задается неравенством. Для этого взять произвольную точку, не лежащую на прямой, подставить ее координаты в неравенство. если неравенство верное, то полуплоскость, содержащая выбранную точку, и является решением исходного неравенства. Если неравенство неверное, то полуплоскость по другую сторону прямой является множеством решений данного неравенства.
- Чтобы решить систему неравенств, необходимо найти область пересечения всех полуплоскостей, являющихся решением каждого неравенства системы.
Эта область может оказаться пустой, тогда система неравенств не имеет решений, несовместна. В противном случае говорят, что система совместна.
Решений может быть конечное число и бесконечное множество. Область может представлять собой замкнутый многоугольник или же быть неограниченной.
Рассмотрим три соответствующих примера.
Пример 1. Решить графически систему:
x + y – 1 ≤ 0;
–2 x – 2y + 5 ≤ 0.
Решение:
- рассмотрим уравнения
x+y–1=0и–2x–2y+5=0, соответствующие неравенствам; - построим прямые, задающиеся этими уравнениями.
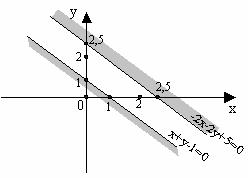
Рисунок 2
Определим полуплоскости, задаваемые неравенствами. Возьмем произвольную точку, пусть (0; 0). Рассмотрим x+ y– 1 0, подставим точку (0; 0): 0 + 0 – 1 ≤ 0. значит, в той полуплоскости, где лежит точка (0; 0), x + y – 1 ≤ 0, т.е. полуплоскость, лежащая ниже прямой, является решением первого неравенства.
Подставив эту точку (0; 0), во второе, получим: –2 ∙ 0 – 2 ∙ 0 + 5 ≤ 0, т.е. в полуплоскости, где лежит точка (0; 0), –2x – 2y + 5≥ 0, а нас спрашивали, где –2x – 2y + 5 ≤ 0, следовательно, в другой полуплоскости – в той, что выше прямой.
Найдем пересечение этих двух полуплоскостей. Прямые параллельны, поэтому плоскости нигде не пересекаются, значит система данных неравенств решений не имеет, несовместна.
Пример 2. Найти графически решения системы неравенств:
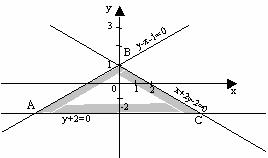
Рисунок 3
1. Выпишем уравнения, соответствующие неравенствам, и построим прямые.
x + 2y– 2 = 0
| x | 2 | 0 |
| y | 0 | 1 |
y – x – 1 = 0
| x | 0 | 2 |
| y | 1 | 3 |
y + 2 = 0;
y = –2.
2. Выбрав точку (0; 0), определим знаки неравенств в полуплоскостях:
0 + 2 ∙ 0 – 2 ≤ 0, т.е. x + 2y– 2 ≤ 0 в полуплоскости ниже прямой;
0 – 0 – 1 ≤ 0, т.е. y –x– 1 ≤ 0 в полуплоскости ниже прямой;
0 + 2 =2 ≥ 0, т.е. y + 2 ≥ 0 в полуплоскости выше прямой.
3. Пересечением этих трех полуплоскостей будет являться область, являющаяся треугольником. Нетрудно найти вершины области, как точки пересечения соответствующих прямых
Таким образом, А(–3; –2), В(0; 1), С(6; –2).
Рассмотрим еще один пример, в котором получившаяся область решения системы не ограничена.
Пример 3. Решить графически систему
Выпишем уравнения, соответствующие неравенствам, и построим прямые.
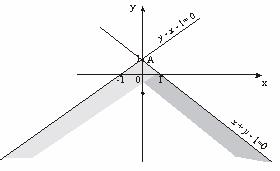
Рисунок 4
x + y – 1 = 0
| x | 0 | 1 |
| y | 1 | 0 |
y – x – 1 = 0
| x | 0 | –1 |
| y | 1 | 0 |
Определим знаки в полуплоскостях. Выберем точку (0; 0):
0 – 0 – 1 ≤ 0, т.е. y – x – 1 ≤ 0 ниже прямой;
0 + 0 – 1 ≤ 0, т.е. x + y – 1 ≤ 0 ниже прямой.
Пересечением двух полуплоскостей является угол с вершиной в точке А(0;1). Эта неограниченная область является решением исходной системы неравенств.

