Решение задачи линейного программирования графически
Определение. Любое решение системы ограничений называется допустимым решением ЗЛП.
Определение. Допустимое решение, в котором целевая функция достигает максимального или минимального значения, называется оптимальным решением.
В силу этих определений задача ЛП может быть сформулирована следующим образом: среди всех точек выпуклой области, являющейся решением системы ограничений, выбрать такую, координаты которой минимизируют (максимизируют) линейную функцию F = с1x + с2y.
Заметим, что переменные x, y в ЗЛП принимают, как правило, неотрицательные значения (x≥ 0, y ≥ 0), поэтому область расположена в I четверти координатной плоскости.
Рассмотрим линейную функцию F = с1x + с2y и зафиксируем какое-нибудь ее значение F. Пусть, к примеру, F = 0, т.е. с1x + с2y = 0. Графиком этого уравнения будет прямая, проходящая через начало координат (0;0) (рис.).
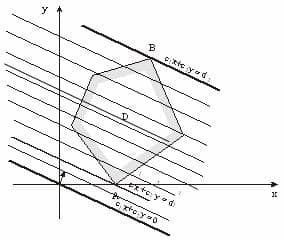
При изменении этого фиксированного значения F = d, прямая с1x+ с2y = d будет смещаться параллельно и «зачертит» всю плоскость. Пусть D – многоугольник – область решения системы ограничений. При изменении d прямая с1x + с2y = d, при некотором значении d = d 1 достигнет многоугольника D, назовем эту точку А «точкой входа», и затем, пройдя многоугольник, при некотором значении d = d2 будем иметь с ним последнюю общую точку В, назовем В «точкой выхода».
Очевидно, что своего наименьшего и наибольшего значения целевая функция F=с1x + с2y достигнет в точках «входа» А и «выхода» В.
Учитывая, что оптимальное значение на множестве допустимых решений целевая функция принимает в вершинах области D, можно предложить следующий план решения ЗЛП:
- построить область решений системы ограничений;
- построить прямую, соответствующую целевой функции, и параллельным переносом этой прямой найти точку «входа» или «выхода» (в зависимости от требования минимизировать или максимизировать целевую функцию);
- определить координаты этой точки, вычислить в них значение целевой функции.
При графическом решении ЗЛП возможны два случая, которые требуют особого обсуждения.
Случай 1
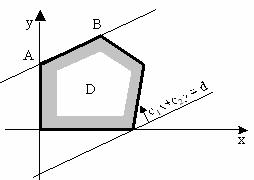
Рисунок 6
При перемещении прямой с1x + с2y= d «вход» или «выход» (как на рисунке) произойдет по стороне многоугольника. Это случится, если в многоугольнике есть стороны, параллельные прямой с1х + с2у = d .
В этом случае точек «выхода» (« входа») бесчисленное множество, а именно – любая точка отрезка АВ. Это означает, что целевая функция принимает максимальное(минимальное) значение не в одной точке, а во всех точках, лежащих на соответствующей стороне многоугольника D.
Случай 2
Рассмотрим случай, когда область допустимых значений неограниченна.
В случае неограниченной области целевая функция может быть задана таким образом, что соответствующая ей прямая не имеет точки «выхода» (или «входа»). Тогда максимальное значение функции (минимальное) не достигается никогда – говорят, что функция не ограничена.
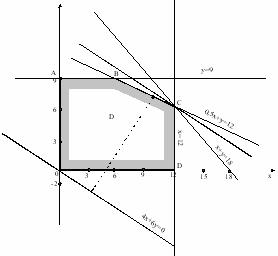
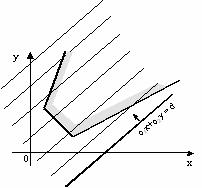
Рисунок
Необходимо найти максимальное значение целевой функции F = 4x+6y → max , при системе ограничений
x+y≤18
0,5x+y≤12
x≤12
y≤9
x≥0, y≥0
Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами.
x + y = 18
|
x |
12 |
9 |
|
y |
6 |
9 |
0,5x + y = 12
|
x |
12 |
18 |
|
y |
6 |
3 |
x = 12 – параллельна оси OY ;
y = 9 – параллельна оси OX ;
x = 0 – ось OY ;
y = 0 – ось OX;
x≥ 0 – полуплоскость правее оси OY;
y ≥ 0 – полуплоскость выше оси OX;
y ≤ 9 – полуплоскость ниже y = 9;
x≤ 12 – полуплоскость левее x = 12;
0,5x + y≤ 12 – полуплоскость ниже прямой 0,5x + y = 12;
x + y≤ 18 – полуплоскость ниже прямой x + y = 18.
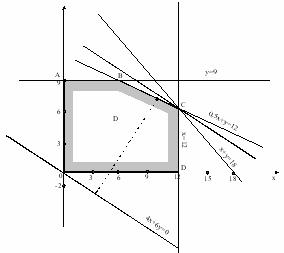
Пересечением всех этих полуплоскостей является очевидно, пятиугольник ОАВСД, с вершинами в точках О(0; 0), А(0; 9), В(6; 9), С(12; 6), Д(12; 0). Этот пятиугольник и образует область допустимых решений задачи.
Рассмотрим целевую функцию задачи F = 4x + 6y → max.
|
x |
3 |
0 |
|
y |
–2 |
0 |
Построим прямую, отвечающую значению функции F = 0 : 4x + 6y = 0. Будем двигать эту прямую параллельным образом.
Из всего семейства прямых 4x+ 6y = const последней вершиной, через которую пройдет прямая при выходе за границу многоугольника, будет вершина С (12; 6). Именно в ней F = 4x + 6y достигнет своего максимального значения.
Значит, при x = 12, y = 6 функция F достигает своего максимального значения F = 4 ∙ 12 + 6 ∙ 6 = 84, равного 84. Точка с координатами (12; 6) удовлетворяет всем неравенствам системы ограничений, и в ней значение целевой функции оптимально F* = 84 (оптимальное значение будем обозначать «*»).
Задача решена. Итак, необходимо выпустить 12 изделий I вида и 6 изделий II вида, при этом прибыль составит 84 тыс. руб.
Графический метод применяется для решения задач, которые имели в системе ограничений только две переменные. Этот метод может применяться и для систем неравенств, имеющих три переменных. Геометрически ситуация будет иная, роль прямых будут играть плоскости в трехмерном пространстве, а решением неравенства от трех переменных будет являться полупространство, находящееся по одну сторону от плоскости. Роль областей будут играть многогранники, являющиеся пересечением полупространств.
Пример №2. Шахта разрабатывает два пласта. Выход штыба по первому пласту составляет а1 %; по второму - а2 %. Максимальная производительность очистного забоя по первому пласту составляет В1 тыс.тонн в год, по второму пласту - В2 тыс.тонн в год. По технологии работ добыча со второго пласта не может превышать добычу с первого пласта. Выход штыба по шахте не должен превышать С1 тыс.тонн в год. Общая нагрузка по двум пластам за год должна быть не меньше С2 тыс.тонн в год. Составить математическую модель и построить множество допустимых значений нагрузки по первому и второму пластам за год.
Пример №3. Магазин продает 2 вида безалкогольных напитков : Колу и лимонад. Доход от одной банки колы составляет 5 центов, тогда как доход от одной банки лимонада 7 центов. В среднем магазин за день продает не более 500 банок обоих напитков. Несмотря на то, что колу выпускает известная торговая марка, покупатели предпочитают лимонад, поскольку он значительно дешевле. Подсчитано, что объем продаж колы и лимонада должны соотноситься не менее 2:1 кроме того , известно что магазин продает не менее 100 банок колы в день. Сколько банок каждого напитка должен иметь магазин в начале рабочего дня для максимизации дохода?
Пример №4. Решить задачу линейного программирования приближенно графическим способом с последующим вычислением точного значения и мах(min) значения целевой функции.
Пример №5. Туристской фирме требуется не более а трехтонных автобусов и не более в пятитонных автобусов. Отпускная цена автобусов первой марки 20000 у.е., второй марки 40000 у.е. Туристская фирма может выделить для приобретения автобусов не более с у.е. Сколько следует приобрести автобусов каждой марки в отдельности, чтобы их общая (суммарная) грузоподъёмность была максимальной. Решить задачу графическим методом.
Пример №6. Используя графический метод, найдите оптимальный производственный план в задаче, заданной таблицей.
Пример №7. Решить графическим методом задачу линейного программирования, подвергнув систему ограничений задачи преобразованиям Жордано-Гаусса. Система ограничений задачи имеет вид:
a11x1 + a12x2 + a13x3 + a14x4 + a15x5 = b1
a21x1 + a22x2 + a23x3 + a24x4 + a25x5 = b2
a31x1 + a32x2 + a33x3 + a34x4 + a35x5 = b3
Методические рекомендации. Преобразования Жордано-Гаусса можно выполнить с помощью этого сервиса или через исследование СЛАУ.
Пример №8. Предприятие выпускает два вида продукции А и В, для производства которых используется сырье трех видов. На изготовление единицы изделия А требуется затратить сырья каждого вида а1, а2, а3 кг соответственно, а для единицы изделия В - в1, в2, в3 кг. Производство обеспечено сырьем каждого вида в количестве Р1, Р2, Р3 кг, соответственно. Стоимость единицы изделия А составляет С1 руб., а единицы изделия В - С2 руб. Требуется составить план производства изделий А и В, обеспечивающий максимальную стоимость готовой продукции.
Пример №9. Необходимо найти максимальное значение целевой функции F = 4x+6y → max, при системе ограничений:
x+y≤18
0,5x+y≤12
x≤12
y≤9
x≥0, y≥0
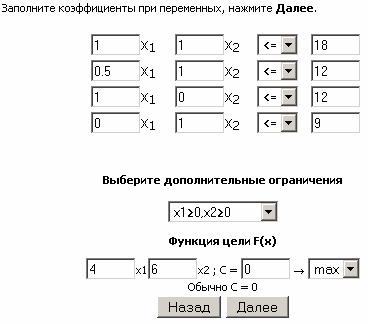
Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого выбираем количество ограничений равное 4 (рисунок 1).

Затем заполняем коэффициенты при переменных и сами ограничения (рисунок 2).
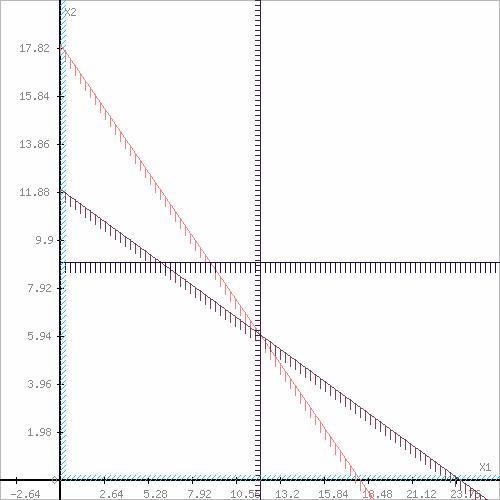
x = 12 – параллельна оси OY;
y = 9 – параллельна оси OX;
x> = 0 – ось OY
y = 0 – ось OX;
x≥ 0 – полуплоскость правее оси OY;
y≥0 – полуплоскость выше оси OX;
y ≤ 9 – полуплоскость ниже y = 9;
x≤ 12 – полуплоскость левее x = 12;
0,5x + y≤ 12 – полуплоскость ниже прямой 0,5x + y = 12;
x + y≤ 18 – полуплоскость ниже прямой x + y = 18.
Пересечением всех этих полуплоскостей является пятиугольник ABCDE, с вершинами в точках A(0; 0), B(0;9), C(6; 9), D(12;6), E(12;0). Этот пятиугольник и образует область допустимых решений задачи.
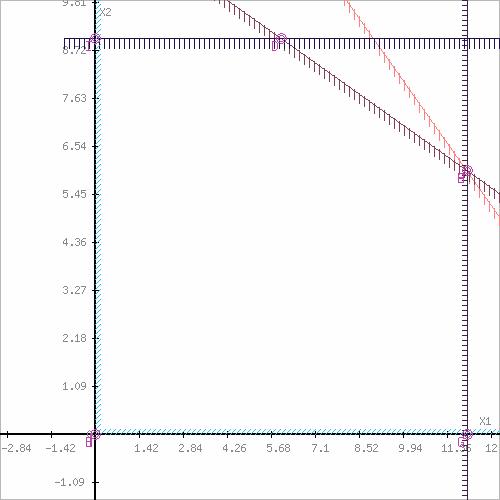
Рассмотрим целевую функцию задачи F = 4x+6y → max.
|
x |
3 |
0 |
|
y |
–2 |
0 |
Построим прямую, отвечающую значению функции F = 0 : 4x + 6y = 0. Будем двигать эту прямую параллельным образом. Из всего семейства прямых 4x + 6y = const последней вершиной, через которую пройдет прямая при выходе за границу многоугольника, будет вершина С (12; 6). Именно в ней F = 4x + 6y достигнет своего максимального значения.
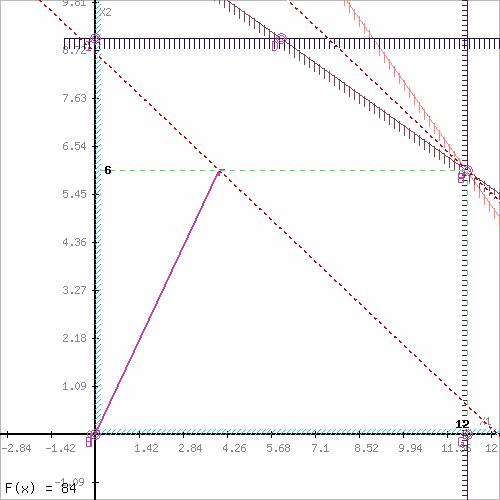
см. также Решение задачи линейного программирования графически online


