Решение задач линейного программирования
Назначение сервиса. Онлайн-калькулятор предназначен для решения задач линейного программирования симплексным методом путем перехода к КЗЛП и СЗЛП. При этом задача на минимум целевой функции сводятся к задаче на поиск максимума через преобразование целевой функцииF*(X) = -F(X). Также имеется возможность составить двойственную задачу.
Решение происходит в три этапа:
- Переход к КЗЛП. Любая ЗЛП вида ax ≤ b, ax ≥ b, ax = b (F(X) → extr) сводится к виду ax = b, F(X) → max;
- Переход к СЗЛП. КЗЛП вида ax = b сводится к виду ax ≤ b, F(X) → max;
- Решение симплексным методом;
Как привести задачу линейного программирования к канонической форме
Как привести каноническую задачу линейного программирования к стандартной форме
Переход от задачи минимизации целевой функции к задаче максимизации
Задача минимизации целевой функции F(X) легко может быть сведена к задаче максимизации функции F*(X) при тех же ограничениях путем введения функции:F*(X) = -F(X). Обе задачи имеют одно и то же решение X*, и при этом min(F(X)) = -max(F*(X)).
Проиллюстрируем этот факт графически:
F(x) → min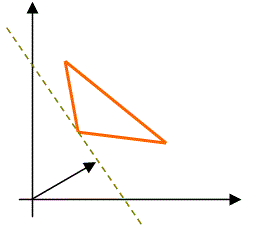 |
F(x) → max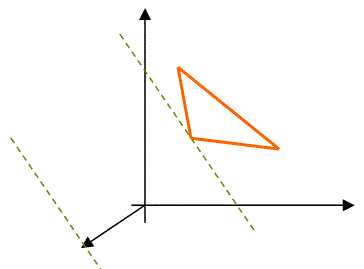 |
Опорный план – план с определёнными через свободные базисными переменными.
Базисный план – опорный план с нулевыми базисными переменными.
Оптимальный план – базисный план, удовлетворяющий оптимальной функции цели (ФЦ).
Ведущий (разрешающий) элемент – коэффициент свободной неизвестной, которая становится базисной, а сам коэффициент преобразуется в единицу.
Направляющая строка – строка ведущего элемента, в которой расположена с единичным коэффициентом базисная неизвестная, исключаемая при преобразовании (строка с минимальным предельным коэффициентом, см. далее).
Направляющий столбец – столбец ведущего элемента, свободная неизвестная которого переводится в базисную (столбец с максимальной выгодой, см. далее).
Переменные x1, …, xm, входящие с единичными коэффициентами только в одно уравнение системы, с нулевыми – в остальные, называются базисными или зависимыми. В канонической системе каждому уравнению соответствует ровно одна базисная переменная. Переход осуществляется с помощью метода Гаусса–Жордана. Основная идея этого метода состоит в сведении системы m уравнений с n неизвестными к каноническому виду при помощи элементарных операций над строками.
Остальные n-m переменных (xm+1,…, xn) называются небазисными или независимыми переменными.
Базисное решение называется допустимым базисным решением, если значения входящих в него базисных переменных xj≥0, что эквивалентно условию неотрицательности bj≥0.
Допустимое базисное решение является угловой точкой допустимого множества S задачи линейного программирования и называется иногда опорным планом.
Если среди неотрицательных чисел bj есть равные нулю, то допустимое базисное решение называется вырожденным (вырожденной угловой точкой) и соответствующая задача линейного программирования называется вырожденной.
Пример №1. Свести задачу линейного программирования к стандартной ЗЛП.
F(X) = x1 + 2x2 - 2x3 → min при ограничениях:
4x1 + 3x2 - x3≤10
- 2x2 + 5x3≥3
x1 + 2x3=9
Для приведения ЗЛП к канонической форме необходимо:
1. Поменять знак у целевой функции. Сведем задачу F(X) → min к задаче F(X) → max. Для этого умножаем F(X) на (-1). В первом неравенстве смысла (≤) вводим базисную переменную x4; во втором неравенстве смысла (≥) вводим базисную переменную x5 со знаком минус.
4x1 + 3x2-1x3 + 1x4 + 0x5 = 10
0x1-2x2 + 5x3 + 0x4-1x5 = 3
1x1 + 0x2 + 2x3 + 0x4 + 0x5 = 9
F(X) = - x1 - 2x2 + 2x3
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:
| 4 | 3 | -1 | 1 | 0 | 10 |
| 0 | -2 | 5 | 0 | -1 | 3 |
| 1 | 0 | 2 | 0 | 0 | 9 |
Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x4.
2. В качестве базовой переменной выбираем x2.
Разрешающий элемент РЭ=-2. Строка, соответствующая переменной x2, получена в результате деления всех элементов строки x2 на разрешающий элемент РЭ=-2. На месте разрешающего элемента получаем 1. В остальных клетках столбца x2 записываем нули. Все остальные элементы определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:
| 4-(0 • 3):-2 | 3-(-2 • 3):-2 | -1-(5 • 3):-2 | 1-(0 • 3):-2 | 0-(-1 • 3):-2 | 10-(3 • 3):-2 |
| 0 : -2 | -2 : -2 | 5 : -2 | 0 : -2 | -1 : -2 | 3 : -2 |
| 1-(0 • 0):-2 | 0-(-2 • 0):-2 | 2-(5 • 0):-2 | 0-(0 • 0):-2 | 0-(-1 • 0):-2 | 9-(3 • 0):-2 |
Получаем новую матрицу:
| 4 | 0 | 61/2 | 1 | -11/2 | 141/2 |
| 0 | 1 | -21/2 | 0 | 1/2 | -11/2 |
| 1 | 0 | 2 | 0 | 0 | 9 |
3. В качестве базовой переменной выбираем x3.
Разрешающий элемент РЭ=2. Строка, соответствующая переменной x3, получена в результате деления всех элементов строки x3 на разрешающий элемент РЭ=2. На месте разрешающего элемента получаем 1. В остальных клетках столбца x3 записываем нули. Все остальные элементы определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:
| 4-(1 • 61/2):2 | 0-(0 • 61/2):2 | 61/2-(2 • 61/2):2 | 1-(0 • 61/2):2 | -11/2-(0 • 61/2):2 | 141/2-(9 • 61/2):2 |
| 0-(1 • -21/2):2 | 1-(0 • -21/2):2 | -21/2-(2 • -21/2):2 | 0-(0 • -21/2):2 | 1/2-(0 • -21/2):2 | -11/2-(9 • -21/2):2 |
| 1 : 2 | 0 : 2 | 2 : 2 | 0 : 2 | 0 : 2 | 9 : 2 |
Получаем новую матрицу:
| 3/4 | 0 | 0 | 1 | -11/2 | -143/4 |
| 11/4 | 1 | 0 | 0 | 1/2 | 93/4 |
| 1/2 | 0 | 1 | 0 | 0 | 41/2 |
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (4,2,3).
Соответствующие уравнения имеют вид:
3/4x1 + x4 - 11/2x5 = -143/4
11/4x1 + x2 + 1/2x5 = 93/4
1/2x1 + x3 = 41/2
Выразим базисные переменные через остальные:
x4 = - 3/4x1 + 11/2x5-143/4
x2 = - 11/4x1 - 1/2x5+93/4
x3 = - 1/2x1+41/2
Подставим их в целевую функцию:
F(X) = - x1 - 2(- 11/4x1 - 1/2x5+93/4) + 2(- 1/2x1+41/2)
или
F(X) = 1/2x1 + x5-101/2 → max
Система неравенств:
- 3/4x1 + 11/2x5-143/4 ≥ 0
- 11/4x1 - 1/2x5+93/4 ≥ 0
- 1/2x1+41/2 ≥ 0
Приводим систему неравенств к следующему виду:
3/4x1 - 11/2x5 ≤ -143/4
11/4x1 + 1/2x5 ≤ 93/4
1/2x1 ≤ 41/2
F(X) = 1/2x1 + x5-101/2 → max
Упростим систему.
3/4x1 - 11/2x2 ≤ -143/4
11/4x1 + 1/2x2 ≤ 93/4
1/2x1 ≤ 41/2
F(X) = 1/2x1 + x2-101/2 → max
Пример №2. Найдите сначала графическим методом, а затем симплекс-методом решение задачи
F(X) = x1 + x2 - x3 + x5+15 → max (min) при ограничениях:
-3x1 + x2 + x3=3
4x1 + 2x2 - x4=12
2x1 - x2 + x5=2
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0, x5 ≥ 0


