Графический метод решения задач нелинейного программирования
Графический метод можно использовать для решения задачи нелинейного программирования (НП), которая содержит две переменных х1 и х2, например задачи следующего вида:Z = f(x1, x2) → min (max);
gi(x1, x2) ≤ bi, i=1,m
Чтобы найти ее оптимальное решение, нужно выполнить следующие действия:
- Найти ОДР, определяемую ограничениями задачи. Если окажется, что эта область пуста, то это означает, что задача не имеет решения.
- Построить семейство линий уровня целевой функции f(х1, х2) = C при различных значениях числового параметра С.
- При решении задачи на минимум определить направление убывания, а для задачи на максимум — направление возрастания линий уровня ЦФ.
- Найти точку ОДР, через которую проходит линия уровня с наименьшим в задаче на минимум (соответственно, наибольшим в задачи на максимум) значением параметра С. Эта точка будет оптимальным решением. Если ЦФ не ограничена снизу в задаче на минимум (сверху — в задаче на максимум), то это означает, что задача не имеет оптимального решения.
- Найти координаты точки оптимума и определить в ней значение ЦФ.
Отметим, что в отличие от задачи ЛП точка оптимума в задаче НП не обязательно находится на границе ОДР. Ею также может быть внутренняя точка этого множества.
Пример. В задаче выпуклого программирования требуется:
- найти решение графическим методом;
- написать функцию Лагранжа и найти ее седловую точку, используя решение, полученное графически.
2x1+x2 ≥ 7
x1+2x2 ≥ 5
Решение. 1) Строим два ограничения, тем самым определяя ОДР. Можно использовать этот калькулятор. Также удобно строить ограничения через этот сервис.
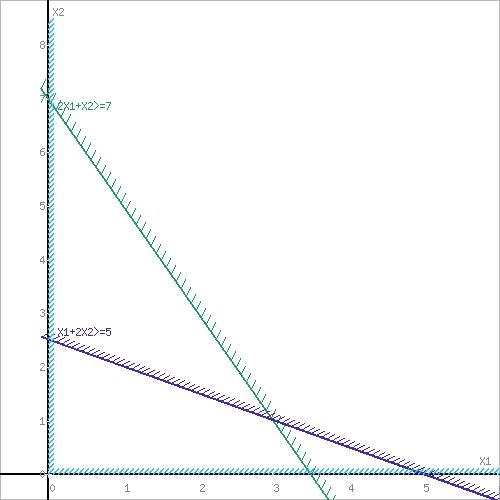
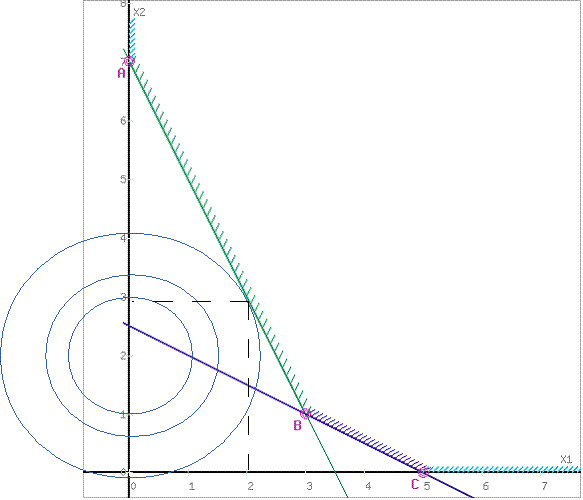
Найдем точку пересечения. Для этого построим уравнение касательной, проходящей через центр окружности O(0;2) и перпендикулярно прямой 2x1+x2-7=0 (можно использовать этот калькулятор). Получаем: 2x2-x1-4=0. Решая систему уравнений:
2x1+x2-7=0
2x2-x1-4=0,
получаем: x1=2, x2=3.
2) Найдем экстремум функции F(X) = x12+(x2-2)2, используя калькулятор Функция Лагранжа
:
L(X, λ)=F(X)+∑(λi·φi)
где F(X) - целевая функция вектора X; φi(X) - ограничения в неявном виде (i=1..n)
В качестве целевой функции, подлежащей оптимизации, в этой задаче выступает функция: F(X) = x12+(x2-2)2
Перепишем ограничение задачи в неявном виде:
φ1(X) = 7 - (2*x1+x2) = 0 (X1)
φ2(X) = 5 - (x1+2*x2) = 0 (X2)
Составим вспомогательную функцию Лагранжа: L(X, λ) = x12+(x2-2)2 - λ1*(7 - (2*x1+x2)) - λ2*(5 - (x1+2*x2))
Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным хi и неопределенным множителям λ.
Составим систему:
∂L/∂x1 = 2*λ1+λ2+2*x1 = 0
∂L/∂x2 = λ1+2*λ2+2*x2-4 = 0
∂L/∂λ1 = 2*x1+x2-7 = 0
∂L/∂λ2 = x1+2*x2-5 = 0
Решив данную систему, получаем:
а) для случая X1: x1 = λ1/2 + λ2 + 2; x2 = 7 - 2x1
Откуда можно найти такие λ1 ≥ 0, λ2 ≥ 0. Пусть λ2 = 0. Тогда λ1 = 2; x1 = 2; x2 = 3.
Поскольку λ2 ≥ 0, то данное решение удовлетворяет условиям Куна-Таккера. Zmin(2;3)=5
б) для случая X2: x2 = λ1/2 + λ2 + 2; x1 = 5 - 2x2
Откуда можно найти такие λ1 ≥ 0, λ2 ≥ 0. Пусть λ2 = 0. Тогда λ1 = 2/5; x1 = 11/5; x2 = 3/5.
Поскольку λ1 ≥ 0, то данное решение удовлетворяет условиям Куна-Таккера. Zmin(11/5;3/5)=6.8
Минимальное значение составит Zmin(2;3)=5.
см. также прикладное использование метода Лагранжа
см. также Решение задачи безусловной оптимизации, Решение классической задачи условной оптимизации.
Пример. Фирма выпускает два вида изделий А и В, которые обрабатываются на станках двух типов. Известны нормативы aij времени, требуемого для обработки одного изделия j-го вида на станке i-го типа (ст./час.), общие фонды рабочего времени каждого типа станков bi (ст./час.). Фирма имеет контракт, согласно которому должна ежедневно поставлять заказчику d1 изделий А и d2 изделий В.
Анализ продаж фирмы показал, что с увеличением объема выпуска из-за роста расходов по реализации изделий их удельная прибыль рj (руб.) уменьшается, причем для ее определения может быть использована формула рj = cj – lхj, где хj — количество проданных изделий j-го вида, а cj и l — фиксированные величины.
Нужно определить, сколько изделий каждого вида следует изготовить фирме, чтобы прибыль от их реализации была максимальной.
Исходные значения параметров представлены в таблице:
| а11 | a12 | a21 | a22 | b1 | b2 | d1 | d2 | c1 | c2 | l |
| 2 | 2 | 6 | 2 | 160 | 220 | 10 | 20 | 320 | 280 | 2 |
1. Составить математическую модель нахождения оптимального плана выпуска продукции.
2. Определить оптимальный план выпуска обобщенным методом множителей Лагранжа и дать экономическую интерпретацию полученных результатов.
Решение:
1. Построение математической модели
В рассматриваемой задаче следует определить
х1 — план выпуска изделий А;
х2 — план выпуска изделий В.
Эти величины являются переменными модели. Обязательства по контракту дают следующие ограничения на их значения: х1 ≥ 10 и х2 ≥ 20. Так как время работы станков каждого типа, затрачиваемое на обработку деталей, не должно превосходить их общего лимита времени работы, то получаем еще два ограничения:
2х1 + 2х2 ≤ 160,
6х1 + 2х2 ≤ 220.
Прибыль Z, получаемая от продажи продукции, вычисляется по формуле
Z = (320 – 2х1) х1 + (280 – 2х2) х2 = 320 х1 – 2x12 + 280 х2 – 2x22.
Таким образом, математическая модель задачи фирмы имеет вид:
Z = 320х1 – 2x12 + 280 х2 – 2x22 → max, (1)
2х1 + 2х2 ≤ 160, (2)
6х1 + 2х2 ≤ 220, (3)
х1 ≥ 10, х2 ≥ 20. (4)
2. Нахождение оптимального плана обобщенным методом множителей Лагранжа.
Сначала проверим, что задача (1) – (4) является задачей ВП. Так как все ограничения модели линейны, для этого достаточно убедиться в том, что ЦФ — вогнутая функция. Для этого вычислим ее гессиан.
Найдем первые частные производные ЦФ:
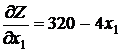и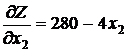 
,
а затем ее вторые частные производные:
;
;
.
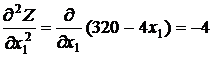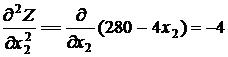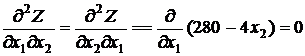Следовательно, гессиан Н функции f имеет следующий вид:
.
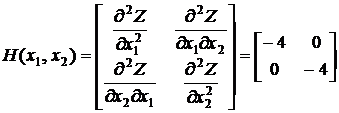Главные миноры первого порядка равны –4, а главный минор второго порядка равен
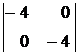= (-4)·(-4) – 0·0 = 16.
Значения этих миноров не зависят от точки х = (x1, x2), причем минор первого (нечетного) порядка отрицателен, а минор второго (четного) порядка положителен. Поэтому ЦФ — строго вогнутая функция (см. теорему 1) Это означает, что задача (1) – (3) является задачей ВП и имеет единственное оптимальное решение.
Для нахождения оптимального решения этой задачи обобщенным методом множителей Лагранжа нужно выполнить следующие действия.
Шаг 1. Сначала решим задачу без учета ограничений, т.е. как задачу отыскания глобального максимума ЦФ. Назовем ее «задача 2.1». Она имеет следующий вид.
Z = 320х1 – 2x12 + 280 х2 – 2x22 → max.
Для ее решения нужно найти стационарную точку ЦФ, координаты которой являются решением системы
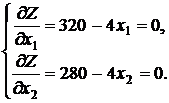
Отсюда, x11=80, x22=70. Таким образом, стационарная точка ЦФ — точка x1=(80,70). В силу вогнутости Z она является точкой ее глобального максимума. Поэтому, если окажется, что эта точка является допустимой в исходной задаче, то она будет ее точкой оптимума. Проверим выполнение ограничения (2):
2×80 + 2×70 = 160 + 140 = 300 > 160.
Найденная точка не является допустимой и, следовательно, не может являться оптимальным решением задачи (1) – (4).
Шаг 2. Согласно схеме обобщенного метода множителей Лагранжа решим задачу максимизации ЦФ («задача 2.2») с учетом первого из ограничений исходной задачи фирмы, которое следует записывать в виде равенства.
Задача 2.2 имеет следующий вид:
Z = 320х1 – 2x12 + 280х2 – 2x22 → max, (5)
2х1 + 2х2 = 160. (6)
Сформируем функцию Лагранжа
L(x1, x2, λ) = 320х1 – 2x12 + 280х2 – 2x22 + λ (160 – 2х1 – 2х2)
и найдем ее стационарные точки. Для этого нужно решить систему
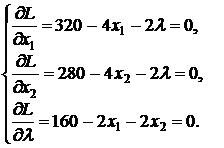
Из первого уравнения имеем
4x1=320-2λ → x1=80-0.5λ,
а из второго уравнения
4x2=280-2λ → x2=70-0.5λ,
Подставив найденные выражения х1 и х2 от λ в третье уравнение, получим
160 – 2×(80 – 0.5λ) – 2×(70 – 0.5λ) = 0 → 2λ – 140 = 0 → λ = 70.
Тогда х1 = 80 – 70/2 = 45, а х2 = 70 – 70/2 = 35, т.е. решение системы:
x12 = 45, x22 = 35, λ2 = 70.
Найденная точка х2 = (45, 35) является оптимальным решением задачи 2.2. Проверим, является ли она допустимой в исходной задаче (1) – (4). Для этого подставим ее координаты в ограничение (3). Получаем, что
6×45 + 2×35 = 270 + 70 = 340 > 220.
Следовательно, найденное решение не является допустимым.
Шаг 3. Решим задачу максимизации ЦФ («задача 2.3») с учетом второго ограничения задачи фирмы, которое также запишем в виде равенства. Она имеет следующий вид:
Z = 320х1 – 2x12 + 280 х2 – 2x22 → max, (7)
6х1 + 2х2 = 220. (8)
Снова сформируем функцию Лагранжа:
L(x1, x2, λ) = 320х1 – 2x12 + 280 х2 – 2x22 + λ (220 – 6х1 – 2х2)
и найдем ее стационарные точки. Для этого нужно решить систему
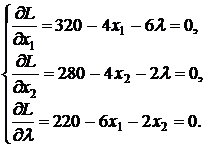
Из первого уравнения имеем
4x1=320-6λ → x1=80-1.5λ,
а из второго уравнения
4x2=280-2λ → x2=70-0.5λ,
Подставив найденные выражения х1 и х2 от λ в третье уравнение, получим
220 – 6 (80 – 1.5λ) – 2×(70 – 0.5λ) = 10λ – 400 = 0 → λ = 40.
Тогда х1 = 80 – 1.5×40 = 20, а х2 = 70 – 40/2 = 50. Итак, решение системы:
x13 = 20, x23 = 50, λ3 = 40.
Найденная точка х3 = (20, 50) является оптимальным решением задачи 3. Проверим, является ли она допустимой в исходной задаче. Для этого подставим ее координаты в ограничение (2). Получаем, что
2×20 + 2×50 = 40 + 100 = 140 < 160,
т.е. это ограничение выполнено. Очевидно, что выполнены и остальные ограничения задачи (1) – (4). Так как она является задачей ВП, это означает, что найдено оптимальное решение задачи фирмы х* = (20, 50). Вычислим оптимальное значение ЦФ:
Z* = 320×20 – 2×202 + 280×50 – 2×502 = 14 600.
Итак, оптимальным решением является выпуск 20 изделий вида А и 50 изделий вида А. Реализация выпущенных изделий даст фирме максимальную прибыль, равную 14 600 руб. Выполнение этой производственной программы требует затрат 140 ст./час. из фонда рабочего времени станков первого типа и 220 ст./час. из фонда рабочего времени станков второго типа. Это означает, что первый вид оборудования недоиспользуется, а второй вид оборудования используется полностью.
Множитель Лагранжа ограничения по станкам второго типа λ* = 40 характеризует предельную полезность этого ресурса. Его величина показывает, что при увеличении фонда рабочего времени станков этого типа на 1 ст./час. прибыль фирмы возрастет примерно на 40 руб.
Геометрическая интерпретация используемого метода решения
С геометрической точки зрения ОДР задачи фирмы представляет собой выпуклый четырехугольник АВCD (см. рис. 2). Линии уровня ЦФ представляют собой концентрические окружности, имеющие общий центр в точке О (80, 70), причем чем дальше от центра находится линия уровня, тем меньшее значение имеет на ней ЦФ.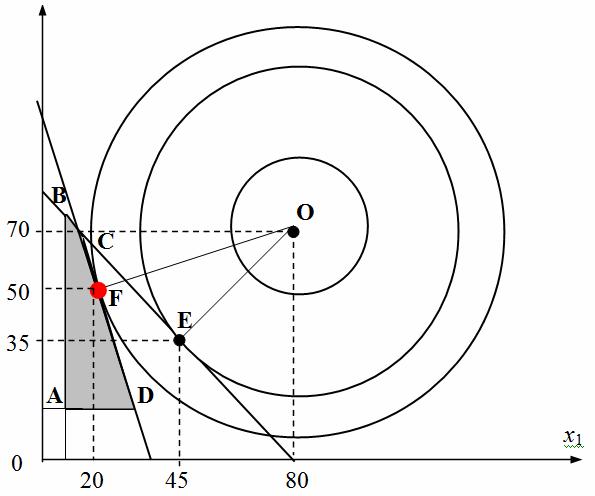
Решение задачи 2.1 — точка О, в которой находится глобальный безусловный максимум ЦФ. Она находится вне ОДР и, следовательно, не является допустимой в задаче фирмы.
Решение задачи 2.2 — точка Е (45, 35), в которой линия уровня ЦФ касается граничной прямой ограничения (2). Эта точка также находится вне ОДР и не является допустимой в задаче фирмы.
Решение задачи 2.3 — точка F (20, 50), в которой линия уровня ЦФ касается граничной прямой ограничения (3). Она лежит на границе ОДР и является «первой» общей точкой ОДР и линии уровня ЦФ. Это оптимальное решение задачи фирмы.
С геометрической точки зрения решение задач 2.2 и 2.3 аналогично графическому решению предыдущей задачи.
Замечание. Если при решении задачи фирмы оказалось бы, что точка О лежит внутри ОДР, то в этом случае точка оптимума была бы глобальным максимумом ЦФ. Возможна ситуация, когда точкой оптимума является угловая точка (одна из вершин ОДР). Она будет стационарной точкой функции Лагранжа в задаче максимизации ЦФ, содержащей два ограничения, активных (выходящих на равенство) в этой точке.
