Решение классической задачи условной оптимизации
Рассмотрим задачу с ограничениями типа равенства:Z = f(x1,…, xn) → min (max); (8)
gi (x1,…, xn) =bi, i=1,m. (9)
Будем считать, что m < n. Определим функцию Лагранжа
L(x, λ) = L(x1,…, xn, λ 1,…, λ m) = f (x1,…, xn) +
λi (bi – gi (x1,…, xn)). (10)
Необходимые условия оптимальности решения задачи (8) – (9) дает следующая теорема.
Теорема 5. Пусть x*=(x*1,...,x*n) — точка локального оптимума задачи (8) ‑ (9), причем все функции f, g1,…, gm непрерывно дифференцируемы в окрестности этой точки и выполнено следующее условие регулярности: градиенты ограничений {
} линейно независимы.
Тогда существует вектор λ*=(λ1,...,λ*m) такой, что вектор (x*, λ*) является стационарной точкой функции Лагранжа, т.е. выполнены соотношения:
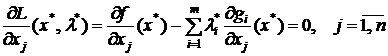; (11)
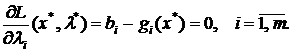(12)
Итак, оптимальное решение задачи (8) ‑ (9) следует искать среди стационарных точек функции Лагранжа. Вектор λ*=(λ*1,...,λ*m) называется вектором множителей Лагранжа. Условие (11) можно записать в векторном виде: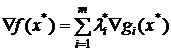 
, где ▽f(x*) = 
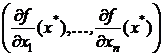— градиент целевой функции. Оно означает, что если точка x* является решением задачи (8) – (9) и выполнено условие регулярности, то в точке оптимума градиент целевой функции представим в виде линейной комбинации градиентов ограничений.
Если задача имеет лишь одно ограничение вида g(x) = b, то условие регулярности автоматически выполнено, а условие (11) означает, что в точке оптимума градиент целевой функции коллинеарен градиенту ограничения, т.е. 
, где λ* — некоторое число. Это значит, что
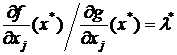для всех 
. (13)
Замечание 1. Если все ограничения задачи линейные, то условие (9) можно записать в матричной форме: Ах = b, где А = (aij) — mxn матрица, а b = (bi) — m‑мерный вектор правых частей ограничений. Тогда условие регулярности означает, что строки матрицы А образуют линейно независимую систему или, что то же самое, матрица А имеет полный ранг, равный m.
