Решение задач нелинейного программирования
Многие зависимости между экономическими показателями имеют нелинейный характер: спрос на товар как функция его цены, зависимость между объемом выпуска и количеством затраченных ресурсов и т.п. Учет этого обстоятельства при построении оптимизационной модели приводит к задаче нелинейной оптимизации, называемой также задачей нелинейного программирования (НП). Далее приводятся необходимые сведения по теории НП.Постановка задачи нелинейной оптимизации
В общем случае задача НП состоит в нахождении экстремума (минимума или максимума) функции
Z = f (x1,…, xn) → min (max), (1)
на множестве, задаваемом ограничениями в виде равенств и (или) неравенств,
gi (x1,…, xn) = bi, i=1,k (2)
gi (x1,…, xn) ≤ bi, i=k+1,m. (3)
Здесь n — число переменных, k — число ограничений типа равенства, m — общее число ограничений, x1,…, xn — переменные, f — целевая функция (ЦФ), gi — функции ограничений, а bi — заданные числа. Ограничения-неравенства включают и условия неотрицательности переменных, если таковые имеются.
Предполагается, что среди функций f и gi (i=1,m) есть хоть одна нелинейная, так как в противном случае (1) – (3) — задача линейного программирования (ЛП).
Любой n-мерный вектор x = (x1,…,xn), удовлетворяющий ограничениям (2) – (3), называется допустимым решением, а множество X всех таких векторов — областью допустимых решений (ОДР).
Простейшей задачей НП является задача безусловной оптимизации, которая состоит в нахождении экстремума (оптимума) нелинейной функции при отсутствии ограничений на значения ее переменных (m = 0). Такие задачи, например, возникают при статистическом оценивании параметров модели.
Другой важный частный случай задачи НП — классическая задача условной оптимизации, в которой все ограничения являются равенствами (k = m).
В отличие от задач ЛП в задачах НП различают два вида оптимумов: локальный и глобальный. Решение задачи НП называется локально оптимальным, если оно является лучшим лишь среди достаточно близких к нему допустимых решений. Если же решение является наилучшим среди всех допустимых решений, то оно называется глобально оптимальным. Дадим точные определения этих понятий.
Точка x*=(x*1,...,x*n) ∈ X называется локальным минимумом (максимумом) функции f на множестве Х, если неравенство f(x*) ≤ f(x) (соответственно f(x*) ≥ f(x)) выполняется для всех х∈Х таких, что
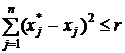для некоторого числа r > 0.
Точка x* называется глобальным минимумом (максимумом) функции f на множестве Х, если неравенство f(x*) ≤ f(x) (соответственно f(x*) ≥ f(x)) выполняется для всех х∈Х.
Если ЦФ имеет несколько локальных оптимумов и принимает на них различные значения, то отыскание среди них глобального оптимума обычно представляет собой сложную проблему. Однако, если целевая функция и ограничения задачи НП обладают свойством «выпуклости», то эта ситуация не возникает.
Функция f называется выпуклой (выпуклой вниз) на выпуклом множестве Х, если для любой пары точек x, y∈Х и любого числа α∈(0, 1) справедливо соотношение
f(α x + (1 – α) y) ≤ α f(x) + (1 – α) f(y). (4)
Функция f называется вогнутой (выпуклой вверх) на выпуклом множестве Х, если для любой пары точек x, y∈Х и любого числа α∈(0, 1) справедливо соотношение
f(α x + (1 – α) y) ≥ α f(x) + (1 – α) f(y). (5)
Функция f называется строго выпуклой (строго вогнутой), если неравенство (4) (соответственно, неравенство (5)) является строгим для всех x ≠ y, т.е. знак неравенства "<" (соответственно, ">").
Ясно, что если f — выпуклая функция, то g = -f — вогнутая функция. Сумма выпуклых (вогнутых) функций — выпуклая (вогнутая) функция. Линейная функция является как выпуклой, так и вогнутой функцией.
Простейший пример выпуклой функции: z = х2, а вогнутой: z =
.
Задача (1) – (3) является задачей выпуклого программирования (ВП), если она удовлетворяет следующим условиям:
1) требуется найти минимум (максимум) выпуклой (вогнутой) целевой функции f ;
2) все функции gi в ограничениях-равенствах (i=1,k) линейные, а в ограничениях-неравенствах (i=k+1,m) выпуклые.
Легко проверить, что если g — выпуклая (вогнутая) функция, то для любого числа b множество {х | g(x) ≤ (≥) b} — выпуклое. Поэтому ОДР в задаче ВП — выпуклое множество. Выпуклым будет и множество оптимальных решений. Если же ЦФ — строго выпуклая (вогнутая) функция, то множество точек ее минимума (максимума) состоит из единственной точки.
Наиболее важное свойство таких задач: любая точка локального оптимума задачи ВП является точкой ее глобального оптимума. Следовательно, в задаче ВП можно говорить об оптимальном решении, не уточняя, идет речь о глобальном или локальном оптимуме.
Поэтому прежде чем начать поиск решения в задаче НП желательно выяснить, является ли она задачей ВП. Положительный ответ на этот вопрос существенно упрощает процедуру нахождения решения, так как в этом случае для нахождения глобального оптимума достаточно найти любой локальный оптимум. Для этого нужно уметь проверять выпуклость (вогнутость) функций, фигурирующих в условиях задачи. Ниже приводятся критерии выпуклости (вогнутости) функций, позволяющие делать такую проверку. Пусть f — дважды непрерывно дифференцируемая функция n переменных. Обозначим
H(x) =
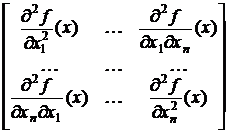(6)
матрицу вторых производных (гессиан) функции f в точке х.
Теорема 1 (условие выпуклости функции). Пусть функция f дважды непрерывно дифференцируема во всех точках выпуклого множества X. Тогда
1) если все главные (угловые) миноры ее гессиана H(x) неотрицательны (положительны) для всех х∈Х, то функция f выпукла (строго выпукла) на Х;
2) если все главные (угловые) миноры ее гессиана H(x) нечетного порядка неположительны (отрицательны), а все главные (угловые) миноры четного порядка неотрицательны (положительны) для всех х∈Х, то функция f вогнута (строго вогнута) на Х.
Пример. Имеется функция f(x1, x2) = 
. Нужно определить, при каких значениях коэффициентов она будет (строго) выпуклой или вогнутой.
Для этого необходимо вычислить ее гессиан. Сначала найдем первые частные производные:
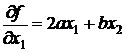и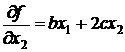 
,
а затем вторые частные производные:
;
;
.
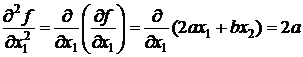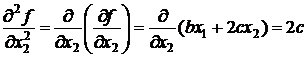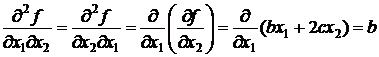Следовательно, гессиан функции f имеет такой вид:
.
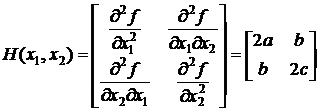Главные миноры первого порядка равны 2а и 2с, а главный минор второго порядка равен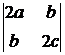 
= 2a·2c – b·b = 4ac – b2. Их значения не зависят от выбора точки х = (x1, x2). Следовательно, функция f будет выпуклой для всех х, если а ≥ 0, с ≥ 0 и 4ac – b2 ≥ 0, и строго выпуклой, если а > 0 и 4ac – b2 > 0. Соответственно, функция f будет вогнутой, если а ≤ 0, с ≤ 0 и 4ac – b2 ≥ 0, и строго вогнутой, если а < 0 и 4ac – b2 > 0.
Для функции одной переменной условия выпуклости имеют следующий вид:
1) функция f (строго) выпукла на множестве Х, если ее вторая производная принимает на Х неотрицательные (положительные) значения, т.е.
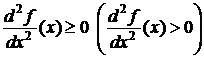для всех х∈Х.
2) функция f (строго) вогнута на множестве Х, если ее вторая производная принимает на Х неположительные (отрицательные) значения, т.е.
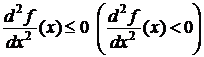для всех х∈Х.