Метод Хука–Дживса
Назначение сервиса. Онлайн-калькулятор предназначен для нахождения минимума функции методом Хука-Дживса. Решение оформляется в формате Word.- Все переменные выражаются через x1,x2
x12+x1x2, записываем как x1^2+x1*x2
Метод Хука-Дживса относятся к категории эвристических методов (методам прямого поиска). Методы прямого поиска используют не менее n независимых направлений, где n-размерность вектора.
Элементарным примером метода, реализующего процедуру рекурсивного перебора на множестве направлений поиска, является метод циклического изменения переменных - каждый раз меняется только одна переменная. Затем вдоль каждого из координатных направлений последовательно проводится поиск точки экстремума на основе методов одномерной минимизации. Однако, если линии уровня ЦФ имеют овражный характер, то процедура поиска становится неэффективной и даже может привести к отсутствию сходимости к точке локального extr, если изменение координатных направлений поиска осуществляется в циклическом порядке (показано Пауэллом).
Модифицированный метод Хука-Дживса позволяет существенно ускорить сходимость за счет того обстоятельства, что поиск периодически проводится в направлении di=xi-xi-1.
По существу процедура Хука–Дживса представляет собой комбинацию двух поисков:
а) исследующий поиск (для выявления характера локального поведения ЦФ и определения направления движения вдоль "оврагов") с циклическим изменением переменных;
б) ускоряющий поиск по образцу с использованием определенных эвристических правил.
Исследующий поиск. Выбирается некоторая исходная точка x0. Задается величина шага ∆i, которая может быть различной для разных координатных направлений и изменяться в процессе поиска.
Если значение ЦФ в пробной точке меньше значения ЦФ в исходной точке, то шаг поиска успешный. В противном случае из исходной точки делается шаг в противоположном направлении. После перебора всех n координат исследующий поиск завершается. Полученная точка называется базовой.
Поиск по образцу. Осуществляется шаг из полученной базовой точки вдоль прямой, соединяющей эту точку с предыдущей базовой. Новая точка образца определяется по формуле:
xpk+1=xk+(xk-xk-1).
Как только движение по образцу не приводит к уменьшению ЦФ, точка xpk+1 фиксируется в качестве временной базовой точки и вновь проводится исследующий поиск. Если в результате получается точка с меньшим значением ЦФ, чем в точке xk, то она рассматривается как новая базовая точка xk+1. Но если исследующий поиск неудачен, то следует вернуться в точку xk и провести исследующий поиск с целью выявления нового направления минимизации. В конечном итоге возникает ситуация, когда такой поиск не приводит к успеху. В этом случае уменьшается шаг путем введения коэффициента α и возобновляется исследующий поиск.
Если исследуемая функция имеет овражный вид, то предпочтительнее использовать метод Хука-Дживса, а не метод Нелдера-Мида, так как в первом методе мы можем регулировать шаг в направлении убывания функции, в то время как во втором методе мы этого сделать не можем.
Схема алгоритма Хука–Дживса
Введем следующие обозначения: xk - текущая базовая точка; xk-1 - предыдущая базовая точка; xpk+1 - точка, построенная при движении по образцу; xk+1 - следующая (новая) базовая точка.Критерий останова: |∆x|≤ε.
Шаг 1. Определить начальную точку x0; приращения (шаги) ∆i; коэффициент уменьшения шага α>1; параметр окончания поиска ε<1.
Шаг 2. Провести исследующий поиск.
Шаг 3. Был ли исследующий поиск удачным (найдена ли точка с меньшим значением ЦФ)?
Да: переход на Шаг 5. Нет: продолжить, т.е. переход на Шаг 4.
Шаг 4. Проверка на окончание поиска. Выполняется ли неравенство |Δx| ≤ ε? Да: окончание поиска, т.е. текущая точка аппроксимирует точку экстремума x*.
Нет: уменьшить приращение ∆i/α; i=1,2,..,n. Переход на Шаг2.
Шаг 5. Провести поиск по образцу: xpk+1=xk+(xk-xk-1).
Шаг 6. Провести исследующий поиск, используя точку xpk+1 в качестве временной базовой точки. Пусть в результате получена точка xk+1.
Шаг 7. Выполняется ли неравенство: f(xk+1) < f(xk)?
Да: положить xk-1= xk; xk= xk+1. Переход на Шаг 5.
Нет: переход на Шаг 4. Пример №1. Найти минимум целевой функции методом Хука–Дживса с точностью ε=0.1.
f(x) = 8x12+4x1x2+522.
Шаг 1. Задаем начальную точку x0=(-4,-4); приращения (шаги): ∆x=(1,1); коэффициент уменьшения шага: α = 2; ε=0.1
Вычислим значение функции в т. x0=(-4,-4)T: f(x0) = 272
Шаг №2. Исследующий поиск.
Фиксируя переменную x2 = -4, дадим приращение x1:
x1=-4 + 1 = -3
f(-3;-4) = 200 < 272
Фиксируя переменную x1 = -3, дадим приращение x2:
x2=-4 + 1 = -3
f(-3;-3) = 153 < 200
Шаг 3. Поиск по образцу.
x1=(-3;-3)T
Так как исследующий поиск был удачным, переходим к поиску по образцу:
x2=x1+(x1-x0) = [-2;-2]
f(x2)=68
Далее проводится исследующий поиск вокруг точки x2.
Шаг №2. Исследующий поиск (после поиска по образцу).
Фиксируя переменную x2 = -2, дадим приращение x1:
x1=-2 + 1 = -1
f(-1;-2) = 36 < 68
Фиксируя переменную x1 = -1, дадим приращение x2:
x2=-2 + 1 = -1
f(-1;-1) = 17 < 36
xk-1 = [-2;-2]
xk = [-1;-1]
Шаг 3. Поиск по образцу.
x2=(-1;-1)T
Так как исследующий поиск был удачным, переходим к поиску по образцу:
x3=x1+(x1-x0) = [0;0]
f(x3)=0
Далее проводится исследующий поиск вокруг точки x3.
Шаг №2. Исследующий поиск (после поиска по образцу).
Фиксируя переменную x2 = 0, дадим приращение x1:
x1=0 + 1 = 1
f(0;0) = 8 > 0
Фиксируя переменную x1 = 0, дадим приращение x2:
x2=0 + 1 = 1
f(0;0) = 5 > 0
Исследующий поиск не был удачным.
Проверка на окончание поиска.
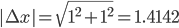
|∆x| = 1.4142 > 0.1
Неравенство не выполняется, поэтому уменьшаем приращение.
∆x1 = 1 / 2 = 0.5
∆x2 = 1 / 2 = 0.5
Шаг №2. Исследующий поиск.
Фиксируя переменную x2 = 0, дадим приращение x1:
x1=0 + 0.5 = 0.5
f(0;0) = 2 > 0
Фиксируя переменную x1 = 0, дадим приращение x2:
x2=0 + 0.5 = 0.5
f(0;0) = 1.25 > 0
Исследующий поиск не был удачным.
Проверка на окончание поиска.
|∆x| = 0.70711 > 0.1
Неравенство не выполняется, поэтому уменьшаем приращение.
∆x1 = 0.5 / 2 = 0.25
∆x2 = 0.5 / 2 = 0.25
Шаг №2. Исследующий поиск.
Фиксируя переменную x2 = 0, дадим приращение x1:
x1=0 + 0.25 = 0.25
f(0;0) = 0.5 > 0
Фиксируя переменную x1 = 0, дадим приращение x2:
x2=0 + 0.25 = 0.25
f(0;0) = 0.313 > 0
Исследующий поиск не был удачным.
Проверка на окончание поиска.
|∆x| = 0.35355 > 0.1
Неравенство не выполняется, поэтому уменьшаем приращение.
∆x1 = 0.25 / 2 = 0.125
∆x2 = 0.25 / 2 = 0.125
Шаг №2. Исследующий поиск.
Фиксируя переменную x2 = 0, дадим приращение x1:
x1=0 + 0.125 = 0.125
f(0;0) = 0.125 > 0
Фиксируя переменную x1 = 0, дадим приращение x2:
x2=0 + 0.125 = 0.125
f(0;0) = 0.0781 > 0
Исследующий поиск не был удачным.
Проверка на окончание поиска.
|∆x| = 0.17678 > 0.1
Неравенство не выполняется, поэтому уменьшаем приращение.
∆x1 = 0.125 / 2 = 0.0625
∆x2 = 0.125 / 2 = 0.0625
Шаг №2. Исследующий поиск.
Фиксируя переменную x2 = 0, дадим приращение x1:
x1=0 + 0.0625 = 0.0625
f(0;0) = 0.0313 > 0
Фиксируя переменную x1 = 0, дадим приращение x2:
x2=0 + 0.0625 = 0.0625
f(0;0) = 0.0195 > 0
Исследующий поиск не был удачным.
Проверка на окончание поиска.
|∆x| = 0.088388 < 0.1
Неравенство выполняется, поэтому прекращаем процесс итераций.
Ответ: x(0;0), f(x)=0