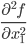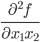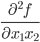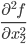Метод Марквардта
Назначение сервиса. Онлайн-калькулятор используется для нахождения минимума функции методом Марквардта. Решение оформляется в формате Word.Правила ввода функции
- Все переменные выражаются через x1,x2
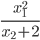≡ x1^2/(x2+2)
Например,
x12+x1x2 ≡ x1^2+x1*x2
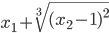≡ x1+(x2-1)^(2/3)
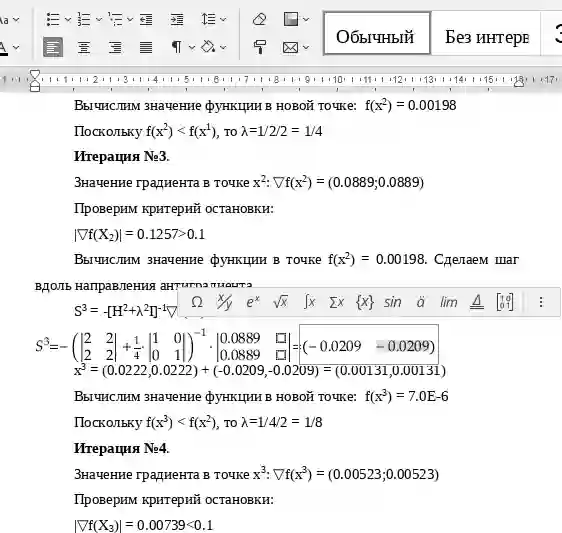
Метод Марквардта (ММ) является комбинацией методов Коши и Ньютона. В нем сочетаются положительные свойства обоих методов. Направление поиска в ММ определяется равенством:
dk=-[Hf(xk)+λk·E]-1·▽f(xk), (1)
где E - единичная матрица.
На начальной стадии λ0 присваивается большое значение (например, 104), так что
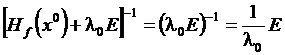. (2)
Таким образом, большим значениям λ0 соответствует направление поиска d(x0)→-▽f(x0), т.е. направление поиска совпадает с направлением антиградиента. Из формулы (2) можно заключить, что при уменьшении λ до нуля направление d(x) изменяется от -▽f(x0) до –Hf-1(x). Если после первого шага получена точка с меньшим значением ЦФ (т.е. f(x1) < f(x0) ), следует выбрать λ1 < λ0 и реализовать еще один шаг. В противном случае следует положить λ0 = β λ0, где β>1 и вновь реализовать предыдущий шаг.
Схема алгоритма Марквардта
Ш. 1 Задать x0 - начальное приближение к x*;
задать M - максимальное (допустимое) количество итераций;
задать ε - параметр сходимости (точность).
Ш. 2 Положить k=0, λ0=104.
Ш. 3 Вычислить ▽f(xk).
Ш. 4 Проверить, выполняется ли критерий останова: |▽f(xk)| ≤ ε.
Да: → Ш.11. Нет: → Ш. 5.
Ш. 5 Проверить, выполняется ли критерий останова: k≥M.
Да: → Ш.11. Нет: → Ш. 6.
Ш. 6 Вычислить d(xk)=-[ Hf(xk)+ λkE]-1▽f(xk)
Ш. 7 Положить xk+1=xk+d(xk).
Ш. 8 Проверить выполнение неравенства: f(xk+1) < f(xk).
Да: → Ш.9. Нет: → Ш. 10.
Ш. 9 Положить λk+1=1/2λk и k=k+1 Ш. 3
Ш. 10 Положить λk=2λk → Ш. 6.
Ш. 11 Печать результатов.
Достоинства метода Марквардта. Относительная простота, ЦФ убывает от итерации к итерации, высокая скорость сходимости в окрестности точки минимума x*, отсутствует процедура поиска вдоль прямой.
Недостатки метода Марквардта. Необходимость вычисления Hf(xk) и последующего решения системы линейных уравнений (1).
Этот метод широко используется при решении задач (например, в регрессионном анализе) в которых f(x) может быть записана в виде суммы квадратов, т.е.
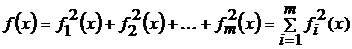. (3)
Пример №1. f(x)=x12+x22+2x1x2+5 → min
Градиент:
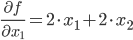
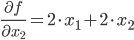
Матрица Гессе:
| Hf = |
|
Значение градиента в точке x0: ▽f(x0) = (4;4)
Проверим критерий остановки:
|▽f(X0)|=<ε
Имеем:
|▽f(X0)| = 5.6569>0.1
Вычислим значение функции в начальной точке f(x0) = 9. Сделаем шаг вдоль направления антиградиента
S1 = -[H0+λ0I]-1▽f(x0)
| S1 = -( |
| +1 |
| )-1 |
| = (-0.8,-0.8) |
Вычислим значение функции в новой точке: f(x1) = 5.16
Поскольку f(x1) < f(x0), то λ=1/2 = 1/2
Итерация №2.
Значение градиента в точке x1: ▽f(x1) = (0.8;0.8)
Проверим критерий остановки:
|▽f(X1)| = 1.1314>0.1
Вычислим значение функции в точке f(x1) = 5.16. Сделаем шаг вдоль направления антиградиента
S2 = -[H1+λ1I]-1▽f(x1)
| S2 = -( |
| +1/2 |
| )-1 |
| = (-0.178,-0.178) |
Вычислим значение функции в новой точке: f(x2) = 5.002
Поскольку f(x2) < f(x1), то λ=(1/2)/2 = 1/4
Итерация №3.
Значение градиента в точке x2: ▽f(x2) = (0.0889;0.0889)
Проверим критерий остановки:
|▽f(X2)| = 0.1257>0.1
Вычислим значение функции в точке f(x2) = 5.002. Сделаем шаг вдоль направления антиградиента
S3 = -[H2+λ2I]-1▽f(x2)
| S3 = -( |
| +1/4 |
| )-1 |
| = (-0.0209,-0.0209) |
Вычислим значение функции в новой точке: f(x3) = 5
Поскольку f(x3) < f(x2), то λ=(1/4)/2 = 1/8
Итерация №4.
Значение градиента в точке x3: ▽f(x3) = (0.00523;0.00523)
Проверим критерий остановки:
|▽f(X3)| = 0.00739<0.1
Пример №2. Найти минимум целевой функции методом Маркварда:
f(x) = (x12 + x22)(exp(-x12-x22)-1)
x = (0;0); x0=(1,5;2)
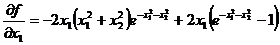
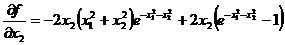
Матрица Гессе: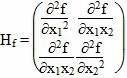 
Итерация №1.
Значение градиента в точке x0: ▽f(x1) = (-3.03;-4.041)
Проверим критерий остановки: |▽f(X1)| = < ε
Имеем: |▽f(X1)| = 5.0507>0.1
Вычислим значение функции в начальной точке f(x0) = -6.2379. Сделаем шаг вдоль направления антиградиента
S1 = -[H0+λ0I]-1▽f(x0)
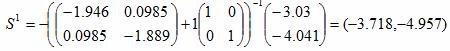
x1 = (1.5,2) + (-3.718,-4.957) = (-2.218,-2.957)
Вычислим значение функции в новой точке: f(x1) = -13.66
Поскольку f(x1) < f(x0), то λ=1/2
Итерация №2.
Значение градиента в точке x1: ▽f(x1) = (4.435;5.914)
Проверим критерий остановки:
|▽f(X1)| = 7.392>0.1
Вычислим значение функции в точке f(x1) = -13.6599. Сделаем шаг вдоль направления антиградиента
S2 = -[H1+λ1I]-1▽f(x1)
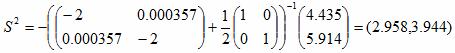
x2 = (-2.218,-2.957) + (2.958,3.944) = (0.741,0.988)
Вычислим значение функции в новой точке: f(x2) = -1.192
Поскольку f(x2) > f(x1), то λ=1/2*2 = 1
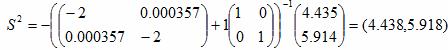
x2 = (0.741,0.988) + (4.438,5.918) = (5.179,6.905)
Вычислим значение функции в новой точке: f(x2) = -74.506
Поскольку f(x2) < f(x1), то λ=1/2
Итерация №3.
Значение градиента в точке x2: ▽f(x1) = (-10.358;-13.811)
Проверим критерий остановки:
|▽f(X1)| = 17.2633>0.1
Вычислим значение функции в точке f(x2) = -74.5058. Сделаем шаг вдоль направления антиградиента
S3 = -[H2+λ2I]-1▽f(x2)
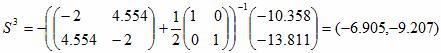
x3 = (5.179,6.905) + (-6.905,-9.207) = (-1.726,-2.302)
Вычислим значение функции в новой точке: f(x3) = -8.276
Поскольку f(x3) > f(x2), то λ=1/2*2 = 1
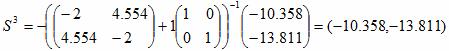
x3 = (-1.726,-2.302) + (-10.358,-13.811) = (-12.084,-16.112)
Вычислим значение функции в новой точке: f(x3) = -405.643
Поскольку f(x3) < f(x2), то λ=1/2
Итерация №4.
Значение градиента в точке x3: ▽f(x1) = (24.169;32.225)
Проверим критерий остановки:
|▽f(X1)| = 40.2811>0.1
Вычислим значение функции в точке f(x3) = -405.6426. Сделаем шаг вдоль направления антиградиента
S4 = -[H3+λ3I]-1▽f(x3)
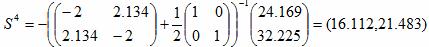
x4 = (-12.084,-16.112) + (16.112,21.483) = (4.028,5.371)
Вычислим значение функции в новой точке: f(x4) = -45.071
Поскольку f(x4) > f(x3), то λ=1/2*2 = 1
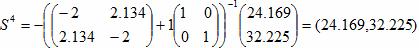
x4 = (4.028,5.371) + (24.169,32.225) = (28.197,37.596)
Вычислим значение функции в новой точке: f(x4) = -2208.499
Поскольку f(x4) < f(x3), то λ=1/2
