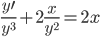Метод допустимых направлений Зойтендейка
Назначение сервиса. Онлайн-калькулятор используется для нахождения минимума функции двух переменных методом допустимых направлений Зойтендейка.- Все переменные выражаются через x1,x2
- Все математические операции выражаются через общепринятые символы (
+,-,*,/,^). Например, x12+x1x2, записываем какx1^2+x1*x2.
Рассмотрим задачу с ограничениями в виде неравенств
f(x) → min,
gi(x)≥0, i=1,m. (1)
Пусть x0 - начальная точка, удовлетворяющая ограничениям:
gi(x0)≥0, i=1,m.
Предположим, что некоторые ограничения являются активными в точке x0:
I0={i:gi(x0)=0, i∈I}, I0⊂I={1,m}.
Вектор d определяет допустимое направление для поиска, если d - направление спуска, т. е.
▽f(x)d < 0 (2)
и точки луча x(α) = x0 + α d, где α ≥ 0 (3)
являются допустимыми на небольшом расстоянии от x0.
Неравенство ▽f(x)d < 0 получается следующим образом.
Разложим в ряд Тейлора функцию f(x) в точке x0:
f(x)=f(x0)+▽fT(x)(x-x0).
В направлении спуска в допустимых точках должно выполняться неравенство: f(x)<f(x0), следовательно, ▽f(x0)(x0)<0.
Вводя обозначение x- x0=d, получим искомый результат.
Точки x(α) будут допустимыми, если для всех активных ограничений выполняется условие:
, (4)
Так как по предположению
gi(x0)=0, ∀i∈I0 и x-x0=d,
то выражение (4) эквивалентно следующему условию для d:
▽gi(x0)·d≥0, ∀i∈I0. (5)
Основная идея: на каждом шаге итерации определяется допустимое направление, т. е. вектор d и скалярный параметр θ>0, такие, чтобы выполнялись следующие неравенства:
▽f(x0)·d≤-θ, ▽gi(x0)·d≥0, ∀i∈I0, (6)
а значение θ выбирается по возможности большим.
При реализации на ЭВМ допустимые направления удобно нормировать, вводя границы
-1≤di≤1, i=1,n. (7)
Такой способ выбора вектора d обеспечивает разумный компромисс между движением внутрь области допустимых значений без нарушения ограничений и движением по направлению наискорейшего спуска.
После того, как вектор d выбран, очередное приближение может быть определено поиском минимального значения α вдоль прямой
x=x0 + α d0(8)
до тех пор, пока либо f(x) не достигнет экстремума, либо пока какое-либо из ограничений не окажется нарушенным.
Обычно для каждого ограничения gi(x)≥0 находятся значения αi>0, при которых
gi(x0 + α·d0)=0, (9)
а затем определяется α как наименьшее из αi: α=min{αi}.
При известном значении α можно использовать любую процедуру одномерного поиска для определения α, которое минимизирует функцию
f(x0+αd0) на отрезке [0, α].
Основной алгоритм Зойтендейка
В данной допустимой точке xt∈S определяется множество индексов тех ограничений, которые активны в xt в пределах заданной погрешности ε , т. е.It={i: 0≤gi(xt)≤ε, i=1,m},
где ε - заданная погрешность.
Полная итерация метода возможных направлений состоит из следующих трех этапов:
Шаг 1. Решить ЗЛП:
θ → max
▽f(xt)·d≤-θ
▽gi(xt)·d≥0, i∈It, -1≤dj≤1, j=1,n.
Пусть dt и θt - полученное решение.
Шаг 2. Если θt ≤ 0, то конец, т. к. дальнейшее улучшение невозможно.
Иначе:
Найти α = min{α: gi(xt+α·dt)=0, i=1,m; α>0}.
Если не существует α>0, положить α=∞, например, α=1010.
При поиске α как min{α: gi(xt+α·dt)=0} может оказаться, что не для всех i=1,m будет выполняться равенство
gi(xt+αdt)=0; значит, мы определяем сразу It множество индексов, для которых gi=0.
Шаг 3. Найти такое αt, что
.
Положить xt+1 = xt + αtdt и продолжить решение.
При определении множества активных ограничений It и α учитывается погрешность, роль которой рассматривается ниже.
Критерии останова процесса итераций:
1. y ≤ 0
2. |▽f(Xk)| < ε
3. Δf(X) = |f(Xk) - f(Xk-1)| < ε
4. ΔX = |Xk - Xk-1| < ε
Пример 1.
f(x)=(x1-3)2+(x2-3)2 → min;
g1=2x1-x²2-1≥0;
g2=9-0.8x²1-2x2≥0;
Начальное допустимое значение x0=(3;-1); f(x0) = 16.
Вычислим градиент в точке x0:
▽f(x0)=[2(x1-3);2(x2-3)] = [0;-8];
▽g1=(2;-2x2) = (2;2);
▽g2=(-1.6x1;-2) = (-4.8;2);
Вычислим значение функций g1 и g2 в точке x0=(3;-1):
g1(3;-1)=4; g2(3;-1)=3.8.
Таким образом, нет активных ограничений: I0={} и первая подзадача принимает вид
θ → max
-8d2 + θ ≤ 0
-1 ≤ di ≤ 1
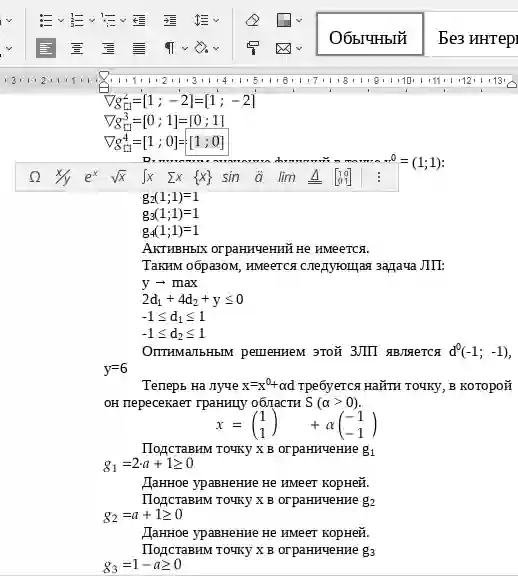
Находим оптимальное решение: θ =8; d*=(0;1)
Теперь на луче x=x0+αd,
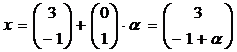, α > 0
требуется найти точку, в которой он пересекает границу области S.
Подставим эту точку в первое ограничение:
g1(x) = 2*3 – (-1+α)2 -1 = α2 - 2α – 4 = 0, -1.2361 ≤ α ≤ 3.2361
С учетом α > 0, получим 0 < α ≤ 3.2361
g2(α) = 9 – 0.8(3)2 – 2(-1+α) = 3.8α – 2, 0 ≤ α ≤ 1.9
Отсюда α = min{3.2361; 1.9} = 1.9
Исследуем отрезок 0 < α ≤ 1.9 для определения экстремальной точки функции
f(α) = (3 - 3)2 + (-1+α-3)2 = (α-4)2 → min
Поэтому α = 4 < 1.9
x1 = x0 + αd = (3; 0.9)
2-я итерация:
x1 = (3; 0.9)
g1(x1) = 4,19
g2(x2) = 0
Таким образом, активное ограничение g2: I0={2}
▽f(x1)=(0;-4.2); ▽g1(x1)=(2;-1.8); ▽g2(x1)=(-4.8;-2);
Далее решается ЗЛП:
θ → max
0*d1 -4.2d2 + θ ≤ 0
-4,8d1 -2d2 - θ ≥ 0
-1 ≤ di ≤ 1
Решение этой задачи d1=(-1;0.774) и θ=3,25.
Поиск на луче x = x1 + αd1
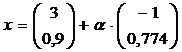, α > 0
требуется найти точку, в которой он пересекает границу области S.
Подставим эту точку в первое ограничение:
g1(x) = 2*(3-α) – (0.9+0.774α)2 -1 = 0.599α2 + 3.393α – 4.19 = 0, -6.706 ≤ α ≤ 1.04
С учетом α > 0, получим 0 < α ≤ 1.04
g2(α) = 9 – 0.8(3-α)2 – 2(0.9+0.774α), 0 M α ≤ 4.065
Отсюда α = min{1.04; 4.065} = 1.04
Исследуем отрезок 0 ≤ α ≤ 1.04 для определения экстремальной точки функции
f(α) = (3-α - 3)2 + (0.9+0.774α -3)2 = 1.599α2 – 3.25α +4.41→ min
Поэтому α = 1.01 < 1.04
x1 = x0 + αd = (1.99; 1.68)
g1(x1) = 0,15
g2(x2) = 2.46
Таким образом, нет активных ограничений: I0={}
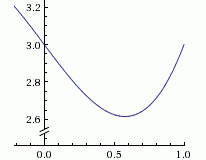
Итеративный процесс можно продолжить подобным образом вплоть до достижения точки минимума x*(2.5; 2) в пределах заданной погрешности. Итерации показаны на рисунке.
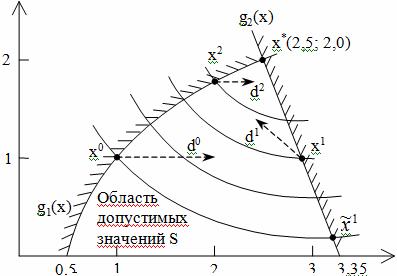
Рис. 1 – Область допустимых значений
В алгоритме Зойтендейка учитываются только активные ограничения в данной допустимой точке, при этом получается зигзагообразный процесс, замедляющий решение, а в некоторых случаях приводящий к "заеданию" - тип ложной сходимости.
К методам, свободным от этих недостатков, можно отнести метод ε-возмущений и метод Топкинса и Вейнотта.
Методами допустимых направлений нельзя непосредственно пользоваться для решения задач с нелинейными ограничениями-равенствами hk(x)=0. В этом случае эти ограничения-равенства необходимо ослабить, допустив ограниченное перемещение вне поверхности, задаваемой ограничениями
- ε ≤ hk(x) ≤ ε.
Однако если ε мало, то одномерный поиск осуществляется небольшими шагами и скорость процесса невелика. С другой стороны, если допускается ограниченное движение вне границ области допустимых значений S, облегчающее выбор допустимого направления, то итеративное решение соответствующих ограничениям уравнений нужно проектировать на область S (рис 2).
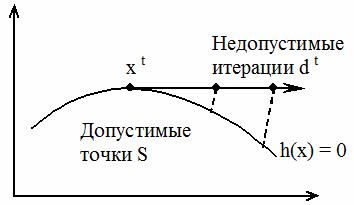
Рис. 2
Другим существенным недостатком метода допустимых направлений является необходимость решения подзадач ЛП.
Источники
- М. Базара, К. Шеттл «Нелинейное программирование. Теория и алгоритмы» М.: Мир 1982
- Д. Химмельблау «Прикладное нелинейное программирование» М.: Мир 1975
