Метод секущих
Если итерации xn и xn+1 расположены достаточно близко друг к другу, то производную f’(xn) в алгоритме Ньютона можно заменить ее приближенным значением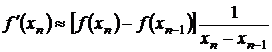 .
.
Таким образом, из формулы метода Ньютона получим формулу секущих
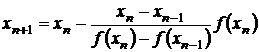
Геометрический смысл такого изменения алгоритма Ньютона состоит в том, что от аппроксимации f(x) касательной мы переходим к секущей (см. рис.).
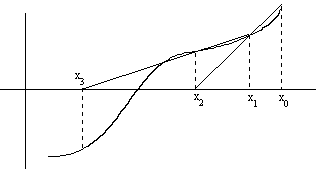
Рисунок - Геометрический смысл метода секущих
Здесь задаются в начале итерационного процесса две точки x0 и x1.
Останов: |xn+1-xn|<ε , где ε - заданная точность.
Достоинства и недостатки метода секущих
Метод секущих уступает методу Ньютона в скорости сходимости, однако не требует вычисления производной функции f(x).
Алгоритм метода секущих
При нахождении нулей функции f, для которой вычисление f'(x) затруднено, часто лучшим выбором, чем метод Ньютона, является метод секущих. В этом алгоритме начинают с двумя исходными числами x1 и х2. На каждом шаге xk+1 получают из xk и xk-1 как единственный нуль линейной функции, принимающей значения f(xk) в xk и f(xk-1) в xk-1. Эта линейная функция представляет секущую к кривой у = f(х), проходящую через ее точки с абсциссами xk и xk-1 - отсюда название метод секущих.Реализация метода секущих на языке программирования Pascal.
procedure secant(var x0, x: real; e: real); var d, y, r: real; begin r := x – x0; d := f(x0); repeat y := f(x); r := r/(d – y)*y; d := y; x := x + r; until abs(r) < e; end;
Перейти к решению своей задачи
Пример решения
Найти нули функции, используя метод секущих.x3-2x-5=0, x Î [1.9, 2.94].
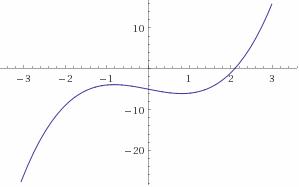
Найдем корни уравнения:
x3-2•x-5 = 0
Находим вторую производную:
d2F/dx2 = 6•x
Уточним интервалы, в которых будут находиться корни уравнения. Для этого исходный интервал [1.9;2.94] разобьем на 10 подынтервалов.
h1 = 1.9 + 1*(2.94-1.9)/10 = 2.004
h2 = 1.9 + (1+1)*(2.94-1.9)/10 = 2.108
Поскольку F(2.004)*F(2.108)<0, то корень лежит в пределах [2.004;2.108].
Вычисляем значения функций в точке a = 2.004.
f(2.004) = -0.96
f ''(2.004) = 12.024
Поскольку f(a)•f ''(a) < 0, то x0 = b = 2.108
Остальные расчеты сведем в таблицу.
| N | x | F(x) | h' = (x-xn-1) / (f(x) - f(xn-1)) | h = f(x)*h' |
| 1 | 2.108 | 0.1512 | 0.09775 | 0.01478 |
| 2 | 2.0932 | -0.0149 | 0.08504 | -0.00127 |
| 3 | 2.0945 | -0.000769 | 0.07837 | -6.0E-5 |
Ответ: x = 2.09454285; F(x) = -9.6E-5




