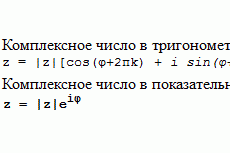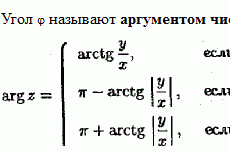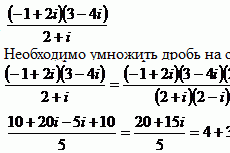Методы минимизации функций
Одномерный поиск
Задача оптимизации функций одной переменной относится к наиболее простому классу оптимизационных задач. Тем не менее, анализ задач такого типа занимает центральное место в оптимизационных исследованиях. Такие задачи обычно решаются в инженерной практике. Вместе с тем, одномерные методы оптимизации часто используются для анализа подзадач, которые возникают при решении многомерных задач оптимизации. Существует большое число алгоритмов решения задач с одной переменной. Классификация методов таких задач основывается на различных предположениях и допущениях относительно природы и свойств функции f(x).Методы исключения интервалов
К данному классу относятся методы: метод равномерного поиска, метод дихотомии, метод золотого сечения, метод Фибоначчи.
Проведем сравнение относительных эффективностей этих методов.
Обозначим длину исходного интервала неопределенности через L1; Ln – длина полученного интервала в результате n-вычислений функций 
– относительное уменьшение первоначального интервала; FR(n)– показатель эффективности.
При использовании метода дихотомии и метода золотого сечения длина получаемого интервала составляет соответственно 
и L1(0,618)n-1 исходного.
Следовательно, относительное уменьшение первоначального интервала неопределенности после n-вычислений значений функции равно:
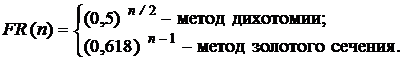
Метод Фибоначчи (МФ) – предельный случай метода золотого сечения (МЗС). Покажем это.
В МЗС:
.
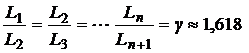В Методе Фибоначчи:
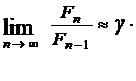
Например, для n = 12 значение g составляет
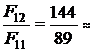1,6179775. Для сравнения рассмотрим метод равномерного поиска (МРП).
, следовательно, 
.
Таблица 4.1 – Величины относительного уменьшения интервала
| Метод поиска | Количество вычислений значений функции | ||||
| n = 2 | n = 5 | n = 10 | n = 15 | n = 20 | |
Дихотомия | 0,5 | 0,177 | 0,031 | 0,006 | 0,0009 |
МЗС | 0,618 | 0,146 | 0,013 | 0,001 | 0,0001 |
МФ | 0,667 | 0,333 | 0,82 | 0,125 | 0,095 |
С другой стороны, можно также сравнивать количество вычислений значений функций, требуемых для достижения заданной точности ε. Если величина
задана, то значение n вычисляется по следующим формулам:
для метода дихотомии:
;
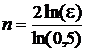для МЗС:
; для МРП: 
.
Таблица 4.2 – Требуемые количества вычислений функции
| Метод поиска | Заданная точность | |||
| e = 0,1 | e = 0,05 | e = 0,01 | e = 0,001 | |
Дихотомия | 7 | 9 | 14 | 20 |
МЗС | 6 | 8 | 11 | 16 |
МФ | 6 | 8 | 11 | 16 |
МРП | 19 | 39 | 199 | 1999 |
