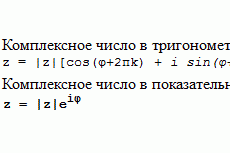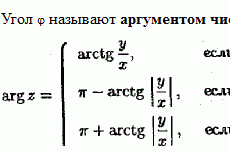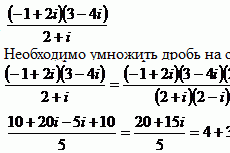Метод непосредственной линеаризации
Назначение сервиса. Онлайн-калькулятор используется для нахождения минимума функции двух переменных методом непосредственной линеаризации.
Правила ввода функций:
- Все переменные выражаются через x1,x2
- Все математические операции выражаются через общепринятые символы (
+,-,*,/,^). Например, x12+x1x2, записываем какx1^2+x1*x2.
Все рассматриваемые ниже методы основываются на разложении нелинейной функции общего вида f(x) в ряд Тейлора до членов первого порядка в окрестности некоторой точки x0:
где
– отбрасываемый член второго порядка малости.
Таким образом, функция f(x) аппроксимируется в точке x0 линейной функцией:
,
где x0 – точка линеаризации.
Замечание. Линеаризацию следует использовать с большой осторожностью, поскольку иногда она дает весьма грубое приближение.
Общая задача нелинейного программирования
Рассмотрим общую задачу нелинейного программирования: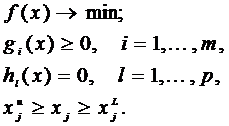
Пусть xt – некоторая заданная оценка решения. Использование непосредственной линеаризации приводит к следующей задаче:
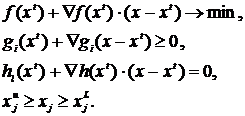
Эта задача представляет собой ЗЛП. Решая ее, находим новое приближение xt+1, которое может и не принадлежать допустимой области решений S.
Если
, то оптимальное значение линеаризованной целевой функции, удовлетворяющее неравенству:
может не быть точной оценкой истинного значения оптимума.
Для сходимости к экстремуму достаточно, чтобы для последовательности точек { xt}, полученных в результате решения последовательности подзадач ЛП, выполнялось следующее условие:
значение целевой функции и невязки по ограничениям в точке xt+1 должно быть меньше их значений в точке xt.
Пример №1.
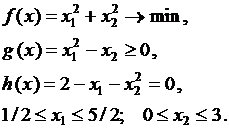
Построим допустимую область S (см. рис.).
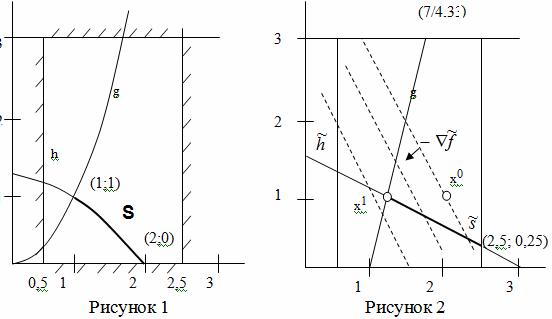
Допустимая область S состоит из точек кривой h(x)=0, лежащей между точкой (2;0), определяемой ограничением x2≥0, и точкой (1;1), определяемой ограничением g(x) ≥0.
В результате линеаризации задачи в точке x0=(2;1) получаем следующую ЗЛП:
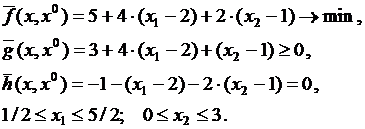
Здесь
представляет собой отрезок прямой 
, ограниченный точками (2.5; 0.25) и (11/9; 8/9). Линии уровня линеаризованной целевой функции представляют собой прямые с наклоном -2, тогда как линии уровня исходной целевой функции – окружности с центром в точке (0;0). Ясно, что решением линеаризованной задачи является точка x1=(11/9; 8/9). В этой точке имеем:
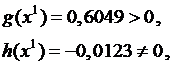
так что ограничение–равенство нарушается. Произведя новую линеаризацию в точке x1, получаем новую задачу:
и 
и имеет координаты x2=(1.0187; 0.9965). Ограничение– равенство ( 
) все еще нарушается, но уже в меньшей степени. Если произвести еще две итерации, то получим очень хорошее приближение к решению x*=(1;1), f(x*)=2
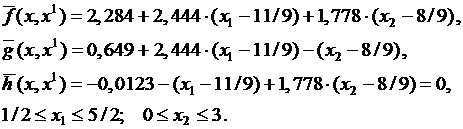
Таблицa - Значения целевой функции для некоторых итераций:
| Итерация | f | g | h |
| 0 | 5 | 3 | –1 |
| 1 | 2,284 | 0,605 | –0,0123 |
| 3 | 2,00015 | 3,44×10-4 | –1,18×10-5 |
| Оптимум | 2 | 0 | 0 |
Из таблицы видно, что значения f,g и h монотонно улучшаются. Однако такая монотонность характерна для задач, функции которых являются "умеренно" нелинейными. В случае функций с ярко выраженной нелинейностью монотонность улучшения нарушается и алгоритм перестает сходиться.
Существует три способа усовершенствования методов непосредственной линеаризации:
1. Использование линейного приближения для отыскания направления спуска.
2. Глобальная аппроксимация нелинейной функции задачи при помощи кусочно–линейчатой функции .
3. Применение последовательных линеаризаций на каждой итерации для уточнения допустимой области S.
