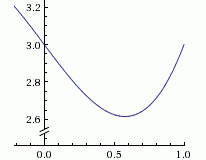
Метод Бройдена–Флетчера–Гольдфарба–Шанно
Назначение сервиса. Онлайн-калькулятор предназначен для нахождения минимума функции методом Бройдена-Флетчера-Шенно (BFGS).Правила ввода функции
- Все переменные выражаются через x1,x2
- Все математические операции выражаются через общепринятые символы +, -, *, /, ^
- Корень квадратный √¯ ≡ sqrt, степень корня ≡ x^(2/3), (x-1)^(1/3)
число π ≡ pi, число e ≡ exp(1), ∞ ≡ infinity
ex = exp(x), log5(x) ≡ log(x,5)
Тригонометрические функции: cos(x), sin(x), tg(x), ctg(x), arccos(x), arcsin(x), arctg(x), arcctg(x)
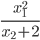≡ x1^2/(x2+2)
Например,
x12+x1x2 ≡ x1^2+x1*x2
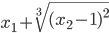≡ x1+(x2-1)^(2/3)
Квазиньютоновские методы также основаны на свойствах квадратичных функций. Данные методы обладают положительными чертами метода Ньютона, однако используют только первые производные.
Итерационный поиск по методу Ньютона осуществлялся по формуле (обобщенный случай с λ):
. (1)
Трудность может возникнуть, когда матрица Гессе 
не является положительно определенной. В этом случае направление перемещения
(2)
может не быть направлением спуска и глобальная сходимость метода не будет обеспечена.
В таких ситуациях обратную матрицу Гессе 
заменяют положительно определенной матрицей Ak, дающей направление перемещения, исходя из градиента ∇f(xk). Отсюда получаем итерационную формулу
, (3)
где λk выбирается так, чтобы минимизировать функцию f(xk+λ·dk) в направлении 
.
Очевидно, что матрица Ak на каждой итерации модифицируется так, чтобы для каждой квадратичной функции вида
(с положительно определенной матрицей 
) матрицы Ak сходились к обращению 
матрицы Гессе функции f(x).
Следовательно, на конечном этапе сходимости мы вновь придем к методу Ньютона.
Если метод применяется к произвольной функции, то Ak может рассматриваться на каждом шаге как аппроксимация (положительно определенная) обращения матрицы Гессе функции f(x).
Для аппроксимации матрицы Hf-1 пользуются следующим рекуррентным соотношением:
Ak+1 = Ak + Ack, (4)
где Ack - корректирующая матрица.
Матрица Ak будет использоваться в формулах (1), (2), (3). Задача заключается в том, чтобы построить матрицу Ak таким образом, чтобы последовательность A0,A1,A2,...,Ak+1 давала приближение к 
. При этом для получения решения x* требуется один дополнительный поиск вдоль прямой, если f(x) - квадратичная функция. Данный подход приводит к успеху при решении задач с нелинейными ЦФ общего вида.
Еще раз напомним свойства квадратичных функций
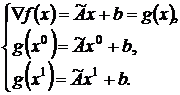
Изменение градиента при переходе из точки x0 в x1 выражается соотношением
или
. (5)
Предположим, что матрица аппроксимируется по формуле
,
где β - скалярная величина. Наиболее предпочтительным является приближение, удовлетворяющее соотношению (5), то есть
Δxk=AkΔgk
Однако построить такую аппроксимацию невозможно, т.к. для того чтобы найти Δgk, необходимо знать матрицу Ak. Здесь используются следующие обозначения:
Δxk=xk+1-xk, Δgk=g(xk+1)-g(xk).
С другой стороны, можно потребовать, чтобы новое приближение удовлетворяло также формуле (5) с учетом свойств квадратичных функций:
, 
. (6)
Подставляя (4) в (6), получим:
.
Выразим отсюда 
:
. (7)
С помощью непосредственной подстановки можно убедиться, что матрица
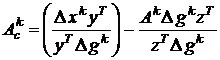(8)
является решением этого уравнения (7). (Для этого надо (8) умножить справа на Δgk, и мы получим выражение (7)).
Здесь y и z - произвольные векторы, т.е. (8) определяет некоторое семейство решений.
Другой способ получения матрицы Ack.
В зависимости от того, имеет матрица Ack ранг 1 или ранг 2, будем говорить о коррекции ранга 1 или ранга 2.
Рассмотрим коррекцию ранга 1:
, (9)
где βk - скаляр, uk - вектор, выбранные так, чтобы выполнялось соотношение:
. (10)
Обозначим 
.
Покажем, как определить βk и uk, чтобы 
. Используя ранее введенное выражение (4) Ak+1=k+Ack, перепишем (10) с учетом (9):
. (11)
Умножим скалярно обе части выражения (11) на γk, получим:
. (12)
Отсюда
. (13)
Используем тождество
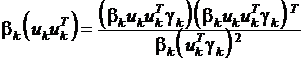(14)
и, осуществив замену
на 
(см. (11));
на 
(см. (13)),
получим формулу коррекции (ранга 1):
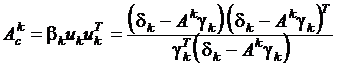. (15)
Далее доказывается теорема о том, что для квадратичной функции f(x) с положительно определенной матрицей A последовательность матриц Ak сходится не более чем за n этапов к обращению матрицы A-1 гессиана функции f(x).
В формуле (8) положим
y=Δxk и z=Ak·Δgk.
Тогда получим:
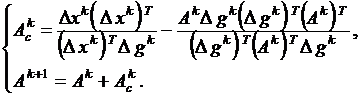(16)
Перепишем формулу (16) в виде:
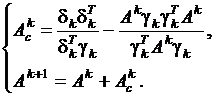. (17)
Матрица Ak+1 удовлетворяет соотношению:
. (18)
Если переставить местами δk и γk в (17) и рассмотреть последовательность матриц
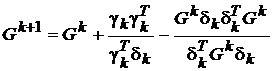, (19)
то полученные матрицы будут удовлетворять соотношению, обратному (17):
. (20)
Таким образом, выражение (19) позволяет построить аппроксимацию самого гессиана (а не его обращения).
Получим формулу для аппроксимации обращения гессиана из (19). После несложных выкладок можно получить выражение:
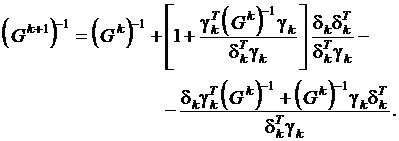(20)
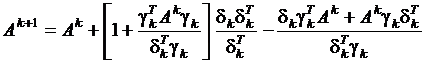(21)
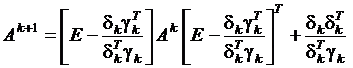. (22)
Полученное уравнение называется симметричной формулой ранга один.
Достоинства: не всегда обязателен возврат к начальной итерации алгоритма и относительно слабая зависимость от точности вычислений одномерного поиска.
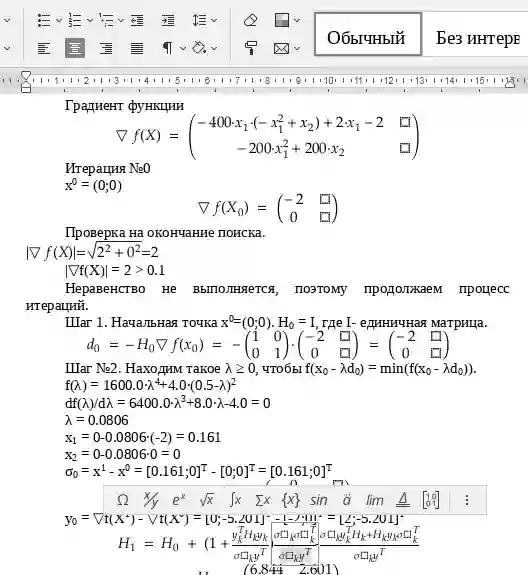
Алгоритм Бройдена–Флетчера–Гольдфарба–Шанно (БФГШ)
1. Выбрать начальную точку x0. ПоложитьН=I, где I- единичная матрица; K = 0.
2. На K-й итерации dK = – HK▽f(xK).
Найти такое λ > 0, чтобы f(xK+ λKdK) = min{f(xK + λdK)}. Положить xK+1 = xK + λKdK; sK = xK+1 – xK; gK = ▽f(xK+1) – ▽f(xK),
.
3. Тест на остановку: если выполнен, то конец. Иначе: выполнить
k=k+1 и возвратиться к 2.