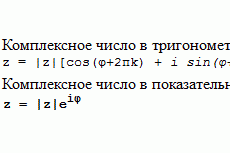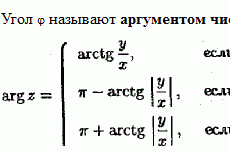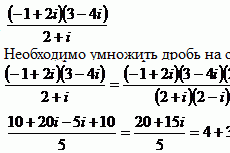Приближенное нахождение корней уравнения
Задание 1. Используя сначала метод секущих, а затем метод касательных, найдите на отрезке [0; 2] с точностью e=0.005 минимум функции: -x^3-1.9*x^2-2.7=0Скачать решение
Задание 2. 1) Выбрав стартовую точку с координатами x01=0.5 и xo2=0.4, примените метод Ньютона–Рафсона, и с точностью e=0.000001 найдите минимум целевой функции:
Скачать решение
2) Выбрав ту же стартовую точку, примените метод наискорейшего спуска, и вновь найдите минимум целевой функции с точностью e=0.0001.
Пример №1. Отделить корни аналитически и уточнить один из них методом половинного деления с точностью до 0,01.
Решение.
sin(x+3.14/3)-x/2=0. Скачать
Пример №2. Определить и найти действительные корни с точностью до 0,001:
а) x4 – 2x – 1 = 0 - методами: 1) деления отрезка пополам; 2) касательных. б) 2log(x) - (x-2)2 = 0 - методами: 1) хорд; 2) итераций.
Решение.
Найдем корни уравнения:
x4-2•x-1 = 0
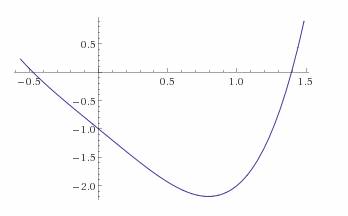
Используем для этого Метод половинного деления (метод дихотомии).
Считаем, что отделение корней произведено и на интервале [a,b] расположен один корень, который необходимо уточнить с погрешностью ε.
Итак, имеем f(a)f(b)<0. Метод дихотомии заключается в следующем.
Определяем половину отрезка c=1/2(a+b) и вычисляем f(c). Проверяем следующие условия:
1. Если |f(c)| < ε, то c – корень. Здесь ε - заданная точность.
2. Если f(c)f(a)<0, то корень лежит в интервале [a,c].
3. Если f(c)f(b)<0, то корень лежит на отрезке[c,b].
Продолжая процесс половинного деления в выбранных подынтервалов, можно дойти до сколь угодно малого отрезка, содержащего корень ξ.
Так как за каждую итерацию интервал, где расположен корень уменьшается в два раза, то через n итераций интервал будет равен:
bn-an=1/2n(b-a)
В качестве корня ξ. возьмем 1/2(an+bn). Тогда погрешность определения корня будет равна (bn – an)/2. Если выполняется условие:
(bn – an)/2 < ε
то процесс поиска заканчивается и ξ = 1/2(an+bn).
Уточним интервалы, в которых будут находиться корни уравнения. Для этого исходный интервал [-1;2] разобьем на 10 подынтервалов.
h1 = -1 + 1*(2-(-1))/10 = -0.7
h2 = -1 + (1+1)*(2-(-1))/10 = -0.4
Поскольку F(-0.7)*F(-0.4)<0, то корень лежит в пределах [-0.7;-0.4].
Итерация 1.
Находим середину отрезка: c = (-0.7 -0.4)/2 = -0.55
F(c) = 0.19
F(x) = 0.64
Поскольку F(c)•F(x) > 0, то a=-0.55
Итерация 2.
Находим середину отрезка: c = (-0.55 -0.4)/2 = -0.48
F(c) = 0.000907
F(x) = 0.19
Поскольку F(c)•F(x) > 0, то a=-0.48
Итерация 3.
Находим середину отрезка: c = (-0.48 -0.4)/2 = -0.44
F(c) = -0.0884
F(x) = 0.000907
Поскольку F(c)•F(x) < 0, то b=-0.44
Итерация 4.
Находим середину отрезка: c = (-0.48 -0.44)/2 = -0.46
F(c) = -0.0442
F(x) = 0.000907
Поскольку F(c)•F(x) < 0, то b=-0.46
Остальные расчеты сведем в таблицу.
| N | c | a | b | f(c) | f(x) |
| 1 | -0.55 | -0.7 | -0.4 | 0.19 | 0.19 |
| 2 | -0.48 | -0.55 | -0.4 | 0.000907 | 0.000907 |
| 3 | -0.44 | -0.48 | -0.4 | 0.000907 | -0.0884 |
| 4 | -0.46 | -0.48 | -0.44 | 0.000907 | -0.0442 |
| 5 | -0.47 | -0.48 | -0.46 | 0.000907 | -0.0217 |
| 6 | -0.47 | -0.48 | -0.47 | 0.000907 | -0.0104 |
| 7 | -0.47 | -0.48 | -0.47 | 0.000907 | -0.00478 |
| 8 | -0.47 | -0.48 | -0.47 | 0.000907 | -0.00194 |
| 9 | -0.47 | -0.48 | -0.47 | 0.000907 | -0.000516 |
x = -0.47; F(x) = -0.000516
Количество итераций, N = 9
Параметр сходимости.
α = (a-b)/N = (-0.48 - (-0.47)/9 = 6.5E-5
h7 = -1 + 7*(2-(-1))/10 = 1.1
h8 = -1 + (7+1)*(2-(-1))/10 = 1.4
Поскольку F(1.1)*F(1.4)<0, то корень лежит в пределах [1.1;1.4].
Итерация 1.
Находим середину отрезка: c = (1.1 + 1.4)/2 = 1.25
F(c) = -1.06
F(x) = -1.74
Поскольку F(c)•F(x) > 0, то a=1.25
Итерация 2.
Находим середину отрезка: c = (1.25 + 1.4)/2 = 1.33
F(c) = -0.57
F(x) = -1.06
Поскольку F(c)•F(x) > 0, то a=1.33
Итерация 3.
Находим середину отрезка: c = (1.33 + 1.4)/2 = 1.36
F(c) = -0.28
F(x) = -0.57
Поскольку F(c)•F(x) > 0, то a=1.36
Итерация 4.
Находим середину отрезка: c = (1.36 + 1.4)/2 = 1.38
F(c) = -0.12
F(x) = -0.28
Поскольку F(c)•F(x) > 0, то a=1.38
Остальные расчеты сведем в таблицу.
| N | c | a | b | f(c) | f(x) |
| 1 | 1.25 | 1.1 | 1.4 | -1.06 | -1.06 |
| 2 | 1.33 | 1.25 | 1.4 | -0.57 | -0.57 |
| 3 | 1.36 | 1.33 | 1.4 | -0.28 | -0.28 |
| 4 | 1.38 | 1.36 | 1.4 | -0.12 | -0.12 |
| 5 | 1.39 | 1.38 | 1.4 | -0.0415 | -0.0415 |
| 6 | 1.4 | 1.39 | 1.4 | -0.000217 | -0.000217 |
| 7 | 1.4 | 1.4 | 1.4 | -0.000217 | 0.0206 |
| 8 | 1.4 | 1.4 | 1.4 | -0.000217 | 0.0102 |
| 9 | 1.4 | 1.4 | 1.4 | -0.000217 | 0.00498 |
x = 1.4; F(x) = 0.00498
Количество итераций, N = 9
Параметр сходимости.
α = (1.4 - 1.4)/9 = 6.5E-5
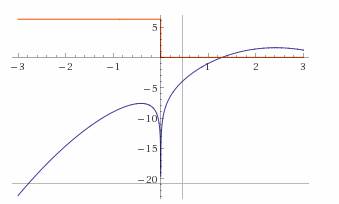
Посмотрите как можно быстро решить задачу.
| Задание | Скачать решение |
| Найти корни уравнения (exp(-x)-x=0), используя Метод итераций | Метод итераций |
| Найти корни уравнения (10*x*exp(2*x) =0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (x^3-x^2+3=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения ((x+3)/(x-2)>0=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (cos(x)^3+sin(x)+tg(x)^4+log(x)^2=0), используя Метод дихотомии | Метод дихотомии |
| Найти методом хорд один из действительных корней уравнения (8*x^4-6*x^3-7*x^2+6*x-1=0) с одним верным знаком после запятой | Метод хорд |
| Найти корни уравнения ((1/3)*x^3-5*x+x*ln(x)=0), используя Метод золотого сечения | Метод золотого сечения |
| Найти корни уравнения ((1/3)*x^3-5*x+x*ln(x)=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (tan(2.5*x)-5*x=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (tan(2.5*x)-5*x=0), используя Комбинированный метод | Комбинированный метод |
| Найти корни уравнения (x^4 - 26*x^3 + 131*x^2-226*x+120=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (2*x^3-9*x^2-60*x+1=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (x^4 - 26*x^3 + 131*x^2-226*x+120=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (x^3 - 3*(x^2) + 4=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (2*x^3-9*x^2-60*x+1=0), используя Метод итераций | Метод итераций |
| Найти корни уравнения (sin(x+3.141592/3)-x/2=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (sin(x+3.141592/3)-x/2=0), используя Метод итераций | Метод итераций |
| Найти корни уравнения (4*x^3-12.3*x^2-x+16.2=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (1/3*x^3-5*x+x*ln(x)=0), используя Метод золотого сечения | Метод золотого сечения |
| Найти корни уравнения (1/3*x^3-5*x+x*ln(x)=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (x^5+((1-cos(100*x))/2)-1/2*atan(x/2)-1=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (x^5+((1-cos(100*x))/2)-1/2*arctan(x/2)-1=0), используя Метод секущих | Метод секущих |
| Найти корни уравнения (18^1/2=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (x^2-18*18=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (x^2-18=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (x^2-18=0), используя Модифицированный метод Ньютона | Модифицированный метод Ньютона |
| Найти корни уравнения (x^2+18=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (x^2+18=0), используя Модифицированный метод Ньютона | Модифицированный метод Ньютона |
| Найти корни уравнения (x^2+18=0), используя Метод итераций | Метод итераций |
| Найти корни уравнения ((x+5)^4=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения ((x+5)^4=0), используя Метод золотого сечения | Метод золотого сечения |
| Найти корни уравнения ((x+5)=0), используя Метод золотого сечения | Метод золотого сечения |
| Найти корни уравнения (sin(x^2)=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (sin(x^2)=0), используя Модифицированный метод Ньютона | Модифицированный метод Ньютона |
| Найти корни уравнения (sin(x^2)=0), используя Метод хорд | Метод хорд |
| Найти корни уравнения (sin(x^2)=0), используя Метод итераций | Метод итераций |
| Найти корни уравнения (sin(x^2)=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (sin(x^2)=0), используя Комбинированный метод | Комбинированный метод |
| Найти корни уравнения (sin(x^2)=0), используя Метод хорд | Метод хорд |
| Найти корни уравнения (-x^2+10=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (x^3-3*x^2+9*x+2=0), используя Метод хорд | Метод хорд |
| Найти корни уравнения (x^3-2*x^2-5*x+6=0), используя Метод итераций | Метод итераций |
| Найти корни уравнения (x^3-2*x^2-5*x+6=0), используя Метод хорд | Метод хорд |
| Найти корни уравнения (x^3-2*x^2-5*x+6=0), используя Комбинированный метод | Комбинированный метод |
| Найти корни уравнения (x^3-2*x^2-5*x+6=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (x^3-3*x^2+3=0), используя Метод хорд | Метод хорд |
| Найти корни уравнения (x^3-x^2+2=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (x^4-4*x^3-8*x^2+1=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (x^4-4*x^3-8*x^2+1=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (x^2-3+0.5^x=0), используя Метод секущих | Метод секущих |
| Найти корни уравнения (x^2-3+0.5^x=0), используя Метод секущих | Метод секущих |
| Найти корни уравнения ((x-2)^2*log(x+11)-1=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения ((x-2)^2*log(x+11)-1=0), используя Метод итераций | Метод итераций |
| Найти корни уравнения ((x-2)^2*log(x+11)-1=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения ((x-2)^2*log(x+11)-1=0), используя Метод хорд | Метод хорд |
| Найти корни уравнения ((x-2)^2*log(x+11)-1=0), используя Метод хорд | Метод хорд |
| Найти корни уравнения ((x-2)^2*log(x+11)-1=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (arccos(0.008*(x*x*x))=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (2*exp(x)-5*x+2 =0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (2*exp(x)-5*x+2 =0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (2*exp(x)-5*x+2 =0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (2*exp(x)-5*x+2 =0), используя Метод хорд | Метод хорд |
| Найти корни уравнения (2*exp(x)-5*x+2 =0), используя Метод итераций | Метод итераций |
| Найти корни уравнения (2*exp(x)-5*x+2=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (2*exp(x)-5*x+2=0), используя Метод золотого сечения | Метод золотого сечения |
| Найти корни уравнения (2*exp(x)-5*x+2=0), используя Метод хорд | Метод хорд |
| Найти корни уравнения (2*exp(x)-5*x+2=0), используя Комбинированный метод | Комбинированный метод |
| Найти корни уравнения (2*exp(x)-5*x+2=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (x^2-tan(0.4*x+0.4)=0), используя Метод хорд | Метод хорд |
| Найти корни уравнения (x^2-tan(0.4*x+0.4)=0), используя Метод секущих | Метод секущих |
| Найти корни уравнения (x^2-tan(0.4*x+0.4)=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (2-x-log(x)=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (x^3-10*x+5=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (x^2-20*sin(x)=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (x^3-10*x+5=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (3x^3-2x+2=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (3*x^3-2*x+2=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (sin(x)-3.141=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (x^2-20*sin(x)=0), используя Метод итераций | Метод итераций |
| Найти корни уравнения (3*x^2-4*x+3=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (0,5*(ln((1+x)/(1-x))+x-1=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (-x-exp(-x)=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (x*log(5)=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (x*log(5)=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (exp(x)+exp(-x)-2*sin(x)=0), используя Метод золотого сечения | Метод золотого сечения |
| Найти корни уравнения (x*x+4*sin(x)-1=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (x*x+4*sin(x)-1=0), используя Метод итераций | Метод итераций |
| Найти корни уравнения (x^3+2*x*x+2=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (exp(x)+exp(-x)-2*sin(x)=0), используя Метод золотого сечения | Метод золотого сечения |
| Найти корни уравнения (x-sin(x)-0.25=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (2*x^3-3*x^2-12*x-5=0), используя Комбинированный метод | Комбинированный метод |
| Найти корни уравнения (log(x)+(x+1)^3=0), используя Метод итераций | Метод итераций |
| Найти корни уравнения (ln(x)+(x+1)^3=0), используя Метод итераций | Метод итераций |
| Найти корни уравнения (x^3-3*x^2+9*x+2=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (x^3-3*x^2+9*x+2=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (x^3-3*x^2+9*x+2=0), используя Метод хорд | Метод хорд |
| Найти корни уравнения (x^3-3*x^2+9*x+2=0), используя Метод золотого сечения | Метод золотого сечения |
| Найти корни уравнения (2*x^3-9*x^2-60*x+1=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (x^3+1,76439*x^2+2,21584*x-3,31344=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения ((expx)-(exp-x)=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (x^4-18*x^2+5*x-8=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (x^4-18*x^2+5*x-8=0), используя Метод хорд | Метод хорд |
| Найти корни уравнения (2^x+5*x-3=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения ((2-3*x)/5*x^2=0), используя Метод итераций | Метод итераций |
| Найти корни уравнения (5*x^3+3*x-2=0), используя Метод итераций | Метод итераций |
| Найти корни уравнения (((2-3*x)/5)^1/3=0), используя Метод итераций | Метод итераций |
| Найти корни уравнения (x^3-1.5*x^2+0.17=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (sin(x)/cos(x)-x/4=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (8*cos(x)-x=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (-8*sin(x)-1=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (x^3-2=0), используя Метод итераций | Метод итераций |
| Найти корни уравнения (x^3-2=0), используя Метод итераций | Метод итераций |
| Найти корни уравнения (sin(x)-0.2*x=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (log(x)*x-x^3+7=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (2*ln(x+7)-5*sin(x)=0), используя Метод хорд | Метод хорд |
| Найти корни уравнения (2*ln(x+7)-5*sin(x)=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (2*ln(x+7)-5*sin(x)=0), используя Метод золотого сечения | Метод золотого сечения |
| Найти корни уравнения ((2*ln(x+7))-(5*sin(x))=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (log(x)*x-x^3+7=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (sinx+logx+x^3+10=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (3+2*x-x^2=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (3+2*x-x^2=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (x^4-18*x^2+6=0), используя Метод хорд | Метод хорд |
| Найти корни уравнения (2*arctan(x)-0.5*x^=0), используя Метод дихотомии | Метод дихотомии |
| Найти корни уравнения (x^2*2^x=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения ((x^2)*(2^x)=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения ((x^2)*(2^x)-1=0), используя Метод Ньютона | Метод Ньютона |
| Найти корни уравнения (cos((1-sin(x))/2+0.5)-x-2=0), используя Метод дихотомии | Метод дихотомии |