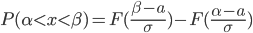Приближенное решение алгебраических уравнений

Приближенное нахождение корней уравнения (1) обычно складывается из двух этапов:
1. Отделение корней, то есть установление интервалов [α_i,β_i], в которых содержится один корень уравнения (1).
2. Уточнение приближенных корней, то есть доведение их до заданной точности.

Для отделения корней полезна след. теорема:
Теорема 1. Если непрерывная функция f(x) принимает значения разных знаков на концах отрезка [a,b], то есть f(a)f(b)<0, то внутри этого отрезка содержится, по меньшей мере, один корень уравнения f(x)=0, то есть найдется хотя бы одно число ξ∈(a,b), такое, что f(ξ)=0.
Корень заведомо единственный, если f ‘(x) существует и сохраняет постоянный знак внутри интервала [a,b].
Доказательство: Пусть для определенности f(a)<0, f(b)>0. Тогда на интервале [a,b] найдется, по крайней мере, одна точка ξ в интервале (ξ₁, ξ₂) (a< ξ₁< ξ< ξ₂<b), на границах которого выполняется
f(ξ₁)<0, f(ξ₂)>0. (2)
В силу непрерывности функции для каждого сколь угодно малого δ>0 всегда найдется число ε>0 такое, что при | ξ ₁- ξ ₂|<ε выполняется |f₁ – f₂|<δ, где f_i=f(ξ_i); i=1,2. Из условия (3.2) и условия |f₁ – f₂|<δ следует, что |f₁|<δ и |f₂|<δ. Поскольку f₁<0, а f₂>0 и f(x) непрерывна, то следовательно существует предел  или f(ξ)=0 и таким образом, первая часть теоремы доказана.
Далее, если f ‘(x) сохраняет знак на [a,b] то она будет монотонна, то есть для любых x₁<x₂ будет выполняться f(x₁)<f(x₂) (если f ‘(x)>0) либо f(x₁) > f(x₂) (если f ‘(x)<0). В силу условия f(a)f(b)<0, монотонности и непрерывности корень будет единственный. Доказательство закончено.
Рассмотрим графический или табличный способ отделения корней. В заданном интервале [a,b] задается сетка a=x₁<x₂<…<x_n=b и вычисляют значения функции f(x_i) (достаточно определить лишь знаки в узлах x_i). Если окажется, что f(x_i)f(x_i+1)<0, то в силу теоремы 1  в интервале (x_i, x_i+1) имеется корень уравнения. Если за корень взять , то точность нахождения корня будет равна половине интервала . Нужно еще убедится, является ли найденный корень единственным. Для этого достаточно провести процесс половинного деления, деля интервал [x_i, x_i+1] на две, четыре и т.д. равных частей и определить знаки функции f(x) в точках деления. При делении мы повышаем точность определения корня.

Пример №1. Определить корни уравнения f(x) = x3 – 6x +2 = 0
Решение: Составляем приблизительную схему.

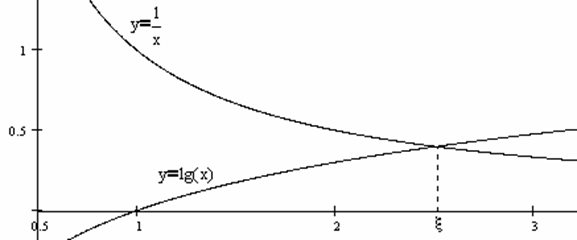
Пример №2. x*lg(x)=1.
Решение: ,
ξ ≈ 2.5.

Итак, мы выделили интервалы, в которых содержится единственный корень. Рассмотрим теперь методы уточнения корней.
Прежде чем перейти к методам уточнения корней, дадим определение сходимости последовательности чисел (или сходимости итерационного процесса).
Определение 1. Если выполняется неравенство
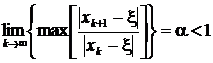, (4)
то говорят, что последовательность {x_k} линейно сходится к пределу ξ. Здесь α - коэффициент сходимости. Если α → 0, то имеем суперлинейную сходимость.

Определение 2. Если существует такое r>1 (r=2,3,…), что 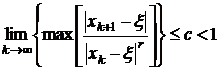, (5)
то последовательность {x_k} имеет сходимость порядка r. Здесь c = const.
Максимум в (4) и (5) берется по всем последовательностям {x_k}.

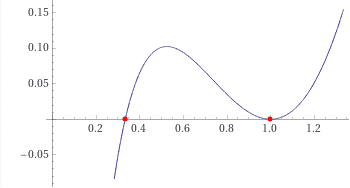
Пример №3. Отделить корни уравнения f(x)=(x-1)2*log(3x), используя графико-аналитический метод. Найти корни уравнения с заданной точностью методами бисекций, Ньютона или простых итераций. Выполнить проверку правильности найденных решений, вычислив невязки.

Решение:
Графически определим приблизительные границы нахождения корней функции. .
Таким образом, имеются два корня в интервалах [0.2;0.4] и [0.8;1.2].
Для проверки решения используем этот калькулятор. Если задать слишком большие границы интервала [-10;10], то решение не получим, поскольку в интервале [-10;0) функция не определена. Можно, либо увеличить количество интервалов разбиения, либо уточнить границы интервала. Если выбрать количество разбиений n=10 , то решение снова не получится, поскольку шаг разбиения будет h=2 и затронет область определения функции:
f(0)= NaN;f (2)= 0.77815
Уточним границы следующим образом: [0;10] при n=40, h= (10-0)/40 = 0.25
Получаем ответ (два корня):

1. Поскольку F(0.25)*F(0.5)<0 (т.е. значения функции на его концах имеют противоположные знаки), то корень лежит в пределах [0.25;0.5].
2. Поскольку F(1) = 0, то корень x = 1