Алгоритм Франка–Вульфа
Назначение сервиса. Онлайн-калькулятор используется для нахождения минимума функции двух переменных f(x1,x2) методом Франка–Вульфа для случая линейных ограниченийax1+bx2 ≤ c.
- Все переменные выражаются через x1,x2
- Все математические операции выражаются через общепринятые символы (
+,-,*,/,^). Например, x12+x1x2, записываем какx1^2+x1*x2. - При этом ограничения типа xi ≥ 0 не учитывайте.
Наиболее простым способом линеаризации является замена общей нелинейной задачи на задачу, получаемую при помощи линеаризации всех функций исходной задачи. Таким образом, получается задача линейного программирования, которую можно решать при помощи методов линейного программирования.
Рассмотрим задачу нелинейного программирования с линейными ограничениями:
f(x) → min, (1)
Ax≤b, x≥0, (2)
где f(x) – нелинейная целевая функция.
Допустимая область S является выпуклым многогранником, образованным пересечением полуплоскостей. Так как f(x) нелинейная, то оптимальное решение может не совпадать с вершиной (или угловой точкой) S. Кроме того, если f(x) не выпуклая, то задача нелинейного программирования может иметь несколько локальных минимумов.
Рассмотрим задачу линейного программирования, полученную линеаризацией исходной задачи нелинейного программирования в некоторой допустимой точке x0∈S:
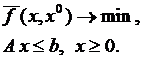
Данная задача линейного программирования имеет оптимальное решение в угловой точке 
.
Важен вопрос о соотношении 
и x*- решением исходной задачи, причем исходная задача может иметь несколько локальных минимумов. Выясним, будет ли 
. В силу допустимости точек x0 и имеет место неравенство:
.
Это следует из того факта, что является минимумом функции 
. Следовательно, если воспользоваться формулой для 
, то получается следующее неравенство:
(3)
. (4)
Очевидно, что вектор
задает направление спуска.
В задаче оптимизации без ограничений использование направления спуска в качестве направления поиска эффективно лишь при применении специальных правил изменения шага или одномерного поиска. Заметим, что одномерный поиск из точки x0 в направлении
приводит к точке . Поскольку является угловой точкой области S и точка x0∈S, то все точки на отрезке прямой между ними также допустимы (т. к. S - выпуклая область). Таким образом, одномерный поиск должен производиться на следующем отрезке прямой:
. (5)
Следовательно, решение задачи линейного программирования, даже не дающее хорошего приближения к экстремуму, позволяет получить важную информацию: определить направление поиска и точки пересечения соответствующего луча с границей допустимой области S.
В результате решения задачи:
(6)
находится точка x1∈S, такая, что f(x1)<f(x0).
Поскольку величина
, то полученная точка x1 может служить точкой линеаризации для построения следующей аппроксимации. Решение последовательности задач линейного программирования и одномерный поиск продолжается до тех пор, пока расстояние между точками последовательных оптимумов xt не станет меньше значения ε.
Алгоритм Франка–Вульфа
Заданы x0 и числа ε>0 и δ>0.Шаг 1: Вычислить
. Если 
конец, иначе Шаг 2.
Шаг 2: Решить следующую задачу линейного программирования:
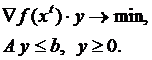
Пусть yt – оптимальное решение этой задачи.
Шаг 3: Найти αt, представляющее собой решение задачи при
.
Шаг 4: Вычислить k.
Шаг 5: Проверить близость к решению. Если
и
, то конец, иначе Шаг 1.
Замечание. В формулировке подзадачи линейного программирования опущены постоянные члены целевой функции f(x,xt).
Пример:
Решение: Пусть x10=2; x20=10 (причем x1,x2∈S). Компоненты вектора-градиента в точке x0 равны:
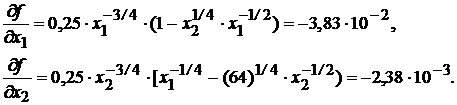
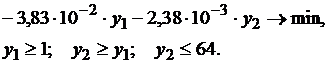
Очевидно, что минимум достигается при наибольших возможных значениях y1 и y1 (y10=64; y20=64).
Шаг 3: Одномерный поиск вдоль прямой:
x=x0+α0(y0-x0) при α∈[0;1].
Используя метод интерполяции, находим α=0.02732.
Шаг 4: Новая точка x1.
x1=(2;10)+0.02732[(64;64)-(2;10)]=(3.694;11.475)
Считаем, что полученное приближение к решению неудовлетворительно, переходим к Шагу 1 следующей итерации.
Шаг 1:
Шаг 2: Подзадача ЛП имеет вид:
3.97*10-3y1-4.56*10-3y2 = min
y1≥1; y2≥y1; y2≤64
Здесь минимум достигается в угловой точке с наименьшим возможным y1 и наибольшим возможным y2; таким образом, y11=1; y21=64.
Шаг 3: Поиск вдоль прямой:
x=x1+α1(y1-x1), α=0.06225
Шаг 4: Новая точка: x2=(3.694;11.475)+0.06225[(1;64)-(3.694;11.475)]=(3.526;14.745)
Продолжая итерации, получим:
x3=(3,924; 15,069), x4=(3,886; 15,710)
Процесс продолжается до тех пор, пока не будет достигнута заданная точность.
Стрелки показывают допустимую область. Из рисунка видно, что в случае оптимума, лежащего внутри допустимой области алгоритм Франка –Вульфа весьма похож на градиентный метод оптимизации без ограничений (зигзагообразная траектория).
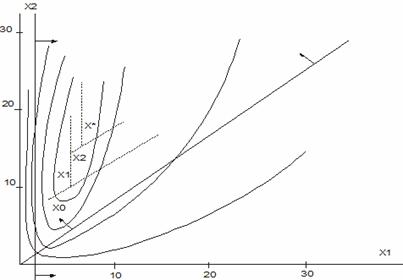
Рисунок 1
