Метод последовательных уступок
Метод (последовательных) уступок заключается в анализе точек на границе Парето и выбора одной из них — компромиссной.Назначение сервиса. Сервис предназначен для онлайн решения многокритериальных задач оптимизации методом последовательных уступок.
Графический метод решения ЗЛП
Решение транспортной задачи
Решение матричной игры
С помощью сервиса в онлайн режиме можно определить цену матричной игры (нижнюю и верхнюю границы), проверить наличие седловой точки, найти решение смешанной стратегии методами: минимакс, симплекс-метод, графический (геометрический) метод, методом Брауна.
Экстремум функции двух переменных
Задачи динамического программирования
Распределить 5 однородных партий товара между тремя рынками так, чтобы получить максимальный доход от их продажи. Доход от продажи на каждом рынке G(X)зависит от количества реализованных партий товара Х и представлен в таблице.
| Объем товара Х (в партиях) | Доход G(X) | ||
| 1 | 2 | 3 | |
| 0 | 0 | 0 | 0 |
| 1 | 28 | 30 | 32 |
| 2 | 41 | 42 | 45 |
| 3 | 50 | 55 | 48 |
| 4 | 62 | 64 | 60 |
| 5 | 76 | 76 | 72 |
Алгоритм метода последовательных уступок (компромиссов)
Вначале производится качественный анализ относительной важности критериев. На основании такого анализа критерии нумеруются в порядке убывания важности.Ищем максимальное значение f1* первого критерия f=f1(x) на всем множестве допустимых решений. Затем назначаем величину «допустимого» снижения (уступки) Δ1 критерия f1(x) и определяем наибольшее значение f2* второго критерия f=f2(x) при условии, что значение первого критерия должно быть не меньше, чем f1(x)-Δ1. Затем назначаем величину «допустимого» снижения (уступки) Δ2 критерия f2(x) и определяем наибольшее значение f3* третьего критерия f=f3(x) при условии, что значение второго критерия должно быть не меньше, чем f2* - Δ2 и т. д. Таким образом, оптимальным решением многокритериальной задачи считается всякое решение последней из задач последовательности:
1) найти
max f1(x)=f1* в области x ∈ X;
2) найти
max f2(x)=f2* в области, задаваемой условиями x ∈ X; f1(x) ≥ f1*-Δ1 (6)
……………………………………………………………….
m) найти
max fm(x)=fm* в области, задаваемой условиями
x ∈ X; fi(x) ≥ fi*-Δi, i=1,...,m-1
Очевидно, что если все Δi=0, то метод уступок находит только лексикографически оптимальные решения, которые доставляют первому по важности критерию наибольшее на Х значение. В другом крайнем случае, когда величины уступок очень велики, решения, получаемые по этому методу, доставляют последнему по важности критерию наибольшее на Х значение. Поэтому величины уступок можно рассматривать как своеобразную меру отклонения приоритета частных критериев от жесткого лексикографического.
Метод последовательных уступок не всегда приводит к получению только эффективных точек, но среди этих точек всегда существует хотя бы одна эффективная. Это следует из следующих утверждений.
Утверждение 3. Если X ⊂ Rn - множество замкнутое и ограниченное, а функции fi(x) непрерывны, то решением m-й задачи из (6) является, по крайней мере, одна эффективная точка.
Утверждение 4. Если x* - единственная (с точностью до эквивалентности) точка, являющаяся решением m-й задачи из (6), то она эффективна.
Примеры решения многокритериальной задачи методом последовательных уступок
Пример №1. Решить методом последовательных уступок многокритериальную задачу.f1(x)=7x1+2x3-x4+x5 → max ,
f2(x)=x1-5x2-4x3+x4 → max
при ограничениях
-x1+x2+x3=2 ;
3x1-x2+x4=3 ;
5x1+2x2+x3+x4+x5=11;
xi ≥ 0 для i=1,2,...,5.
Упорядочим критерии согласно их нумерации, то есть будем в начале работать с критерием f1(x), а затем с критерием f2(x).
При решении примера методом искусственного базиса была получена симплекс-таблица (табл.). Возьмем ее в качестве начальной, вычислив относительные оценки для функции f=f1(x). Получим таблицу 10. Таблица 11 определяет точку, доставляющую функции f1(x) наибольшее значение f1*, равное 16.
Таблица 10. Таблица 11.
7 | 0 | |||||||||
cв | X1 | x2 | x4 | x2 | ||||||
2 | x3 | -1 | 1 | 2 | x3 | 1/3 | 2/3 | 3 | ||
-1 | x4 | 3 | -1 | 3 | x1 | 1/3 | -1/3 | 1 | ||
1 | x5 | 3 | 2 | 6 | x5 | -1 | 3 | 3 | ||
f1 | -9 | 5 | 7 | f1 | 3 | 2 | 16 |
Далее переходим к решению задачи
f2(x)=x1-5x2-4x3+x4 → max
при ограничениях задачи, к которым добавлено новое ограничение f1(x)≥f1*-Δ:
-x1+x2+x3=2,
3x1-x2+x4=3 , (7)
5x1+2x2+x3+x4+x5=11,
7x1+2x3- x4+x5³16-Δ,
xi ≥ 0 для i=1,2,...,5.
Новое ограничение преобразуем в равенство и заменим переменные x1,x3,x5, используя таблицу 11, выражениями
x1=1/3x2-1/3x4+1, x3=-2/3x2-1/3x4+3, x5=-3x2+x4+3.
В результате этих преобразований дополнительно введенное ограничение примет вид -2x2-x4+x6=-16+Δ. Итак, получили задачу параметрического программирования с параметром в правой части ограничений.
В качестве начальной таблицы для задачи (7) можно использовать таблицу 12, которая получена из таблицы 11 в результате пополнения ее еще одной строкой и пересчета строки относительных оценок. Решим задачу (7) для произвольного параметра Δ≥0. Для этого столбец правых частей ограничений в таблице 12 представим в виде двух столбцов z′, z″: zi0=zi′+zi″Δ. При выборе главной строки в таблице 12 следует использовать значения из столбца z′. Полученная далее таблица 13 является оптимальной при Δ=0 и при всех значениях Δ, удовлетворяющих условиям
3+(-1/9) Δ ≥ 0, 1+(-1/9) Δ ≥ 0, 3+1/3 Δ ≥ 0, 0+1/3 Δ ≥ 0.
Из этой системы неравенств получаем 0 ≤ Δ ≤ 9. При этих значениях параметра решением задачи является точка x*=(1+(-1/9)Δ, 0, 3+(-1/9)Δ, 0+1/3Δ, 3+1/3Δ).
Таблица 12. Таблица 13.
1 | -5 | ||||||||||
св | x4 | x2 | z′ | z″ | x6 | x2 | z′ | z″ | |||
-4 | x3 | 1/3 | 2/3 | 3 | 0 | x3 | -1/9 | 4/9 | 3 | -1/9 | |
1 | x1 | 1/3 | -1/3 | 1 | 0 | x1 | -1/9 | -5/9 | 1 | -1/9 | |
0 | x5 | -1 | 3 | 3 | 0 | x5 | 1/3 | 11/3 | 3 | 1/3 | |
0 | x6 | 3 | 2 | 0 | 1 | x4 | 1/3 | 2/3 | 0 | 1/3 | |
f2 | -2 | 2 | -11 | 0 | f2 | 2/3 | 10/3 | -11 | 2/3 | ||
При Δ > 9 таблица 13 не является оптимальной, и нужно выполнить шаг двойственного симплекс-метода с главным элементом, стоящим на пересечение второй строки и первого или второго столбцов. Получим таблицу 14, из которой видно, что при Δ > 9 решениями являются точки, доставляющие функции f2(x) значение –5. Таблица 14 определяет опорное решение x**=(0,0,2,3,6).
Таблица 14.
x1 | x2 | z′ | z″ | ||
x3 | -1 | 1 | 2 | 0 | |
x6 | -9 | 5 | -9 | 1 | |
x5 | 3 | 2 | 6 | 0 | |
x4 | 3 | -1 | 3 | 0 | |
f2 | 6 | 0 | -5 | 0 |
Найдем эти решения. Выберем главным столбец с 0-оценкой. В зависимости от Δ главной строкой будет первая или вторая строка. Если
(-9+Δ)/5 > 2, то главной строкой будет выбрана 1-я. А значит, следующей будет таблица 15. Она определяет опорное решение X=(0,2,0,5,2), если
–19+Δ≥0. Итак, если D≥19, оптимальными решениями будут все точки выпуклой комбинации
ax**+(1-a)x*=(0, 2-2a, 2a,5-2a,2+4a), где a∈[0,1].
Таблица 15.
x1 | x3 | z′ | z″ | ||
x2 | -1 | 1 | 2 | 0 | |
x6 | -4 | -5 | -19 | 1 | |
x5 | 5 | -2 | 2 | 0 | |
x4 | 2 | 1 | 5 | 0 | |
f2 | 6 | 0 | -5 | 0 |
Если (-9+Δ)/5 > 2, то главной строкой будет выбрана 2-я. А значит, следующей после таблицы 14 будет таблица 16. Таблица 16 определяет решение X=(0, (-9+Δ)/5, (19-Δ)/5, (6+Δ)/5, (48-2Δ)/5), если –19+Δ≤0. Итак, если Δ≤19, оптимальными решениями будут все точки выпуклой комбинации
ax**+(1-a)x*=(0, (1-a)(-9+Δ)/5, (19-Δ)/5+a(-9+Δ)/5, (6+Δ)/5+a(9-Δ)/5, (48-2Δ)/5+a(-18+2Δ)/5), где a∈[0,1].
Таблица 16.
x1 | x6 | z′ | z″ | ||
x3 | 4/5 | -1/5 | 19/5 | -1/5 | |
x2 | -9/5 | 1/5 | -9/5 | 1/5 | |
x5 | 33/5 | -2/5 | 48/5 | -2/5 | |
x4 | 6/5 | 1/5 | 6/5 | 1/5 | |
f2 | 6 | 0 | -5 | 0 |
Окончательный результат формулируется следующим образом: решением многокритериальной задачи являются :
точки x*=(1+(-1/9)Δ, 0, 3+(-1/9)Δ, 0+1/3Δ, 3+1/3Δ), если 0 ≤ Δ ≤ 9,
точки x**=(0, (1-a)(-9+Δ)/5, (19-Δ)/5+a(-9+Δ)/5,
(6+Δ)/5+a(9-Δ)/5,(48-2Δ)/5+a(-18+2Δ)/5), если 9 < Δ ≤ 19,
точки x***=(0, 2-2a, 2a,5-2a,2+4a), если Δ ≥ 19,
где a∈[0,1].
Пример №2. Методом последовательных уступок найти решение задачи, считая, что критерии упорядочены по важности в последовательности {f2,f1}, и Δ2=1.
f1=-x1+3x2 → max,
f2(x)=4x1-x2 → max ,
Первая задача из последовательности (6) в данном случае имеет вид:
f2(x)=4x1-x2 → max ,
при ограничениях
-x1+x2≤1, x1+x2≥3, x1-2x2≤0 , x1≤4 , x2≤3.
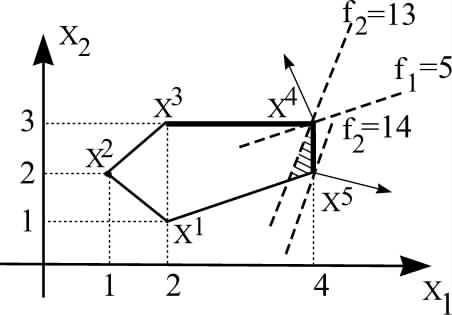
Решение этой задачи можно найти графически. Из рисунка 14 видно, что максимум критерия f2(x) на множестве X достигается в вершине x5=(4,2) и f2*=f2(x5)=14.
Графическое решение примера №2.
Добавим к ограничениям задачи условие f2≥f2*-Δ и сформулируем вторую задачу последовательности (6):
f1=-x1+3x2 → max,
-x1+x2≤1 ,x1+x2≥3, x1-2x2≤0 ,x1≤4 ,x2≤3,
4x1-x2≥13
Ее решением (рис.) будет вершина x4=(4,3) и f1*=f1(x4)=5. Так как, оптимальное решение последней задачи единственно, то в силу утверждения 5, x4 принадлежит множеству Парето.
Отметим, что при Δ∈[0,1] методом последовательных уступок будет найдена одна из точек отрезка [x4,x5], а при Δ>1, одна из точек отрезка [x3,x4]. Все эти точки и только они принадлежит множеству Парето.
Пример №2. Математическая модель трехкритериальной задачи имеет вид:
Z1=аx1+ x2– 3x3→max;
Z2=x1+ 3x2– 2x3→min;
Z3= –x1+ 2x2+аx3→max;
x1+ 3x2+2x3≥1,
2x1–x2+x3≤а,
x1+ 2x2≤24,
x1, x2, x3≥0.
Решить задачу методом последовательных уступок, выбрав уступку по первому критерию d1=4, а по второму d2=5.