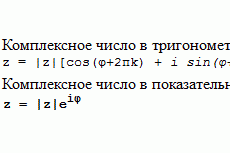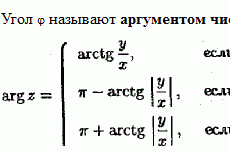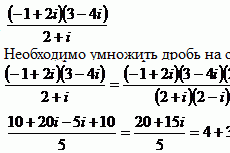Метод Свенна
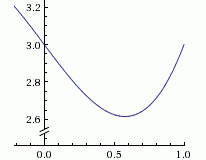
С помощью метода Свенна получают начальный интервал локализации минимума.
Для получения решения в онлайн режиме необходимо заполнить исходные данные.
Примеры правильного написания F(x):
1)
2)
3) Корень квадратный как sqrt(), π ≡ pi.
1)
10•x•e2x записываем как: 10*x*exp(2*x)
2)
x•e-x+cos(3x) ≡ x*exp(-x)+cos(3*x), x3-x2+3 ≡ x^3-x^2+3
3) Корень квадратный как sqrt(), π ≡ pi.
Алгоритм метода Свенна
Начальный этап:1) задать x0 – произвольная начальная точка.
2) выбрать шаг h.
Основной этап:
Шаг 1:
Установить направление убывания целевой функции. Для этого надо взять x2=x1+h. Если f1<f2, то надо поменять направление движения(h=-h и взять x2=x1+h).
Шаг 2:
Вычислять fk в точках xk+1=xk+hk, где hk=2hk-1, k=2,3,…,n-1 до тех пор пока не прид¨м в точку xn такую что fn>fn-1.
Шаг 3:
Установить начальный интервал локализации минимума a1=xn-2 и b1=xn.