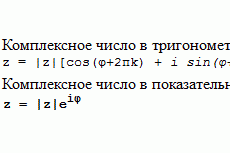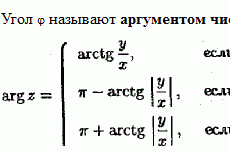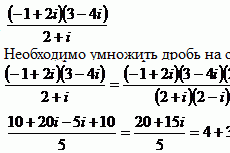Формула прямоугольников
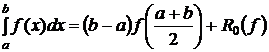
Оценка остаточного члена формулы:
, 
или 
.
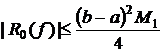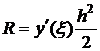Назначение сервиса. Сервис предназначен для онлайн вычисления определенного интеграла по формуле прямоугольников.
Инструкция. Введите подынтегральную функцию f(x), нажмите Решить. Полученное решение сохраняется в файле Word. Также создается шаблон решения в Excel. Ниже представлена видеоинструкция.
Правила ввода функции
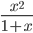≡ x^2/(1+x)
cos2(2x+π) ≡ (cos(2*x+pi))^2
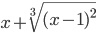≡ x+(x-1)^(2/3)
Формула средних прямоугольников
Это самая простая квадратурная формула вычисления интеграла, в которой используется одно значение функции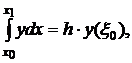
(1)
где
; h=x1-x0.
Формула (1) представляет собой центральную формулу прямоугольников. Вычислим остаточный член. Разложим в ряд Тейлора функцию y=f(x) в точке ε0:
(2)
где ε1[x,ε0]; x∈[x0,x1]. Проинтегрируем (2):
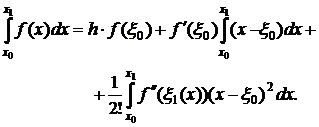(3)
Во втором слагаемом подынтегральная функция нечетная, а пределы интегрирования симметричны относительно точки ε0. Поэтому второй интеграл равен нулю. Таким образом, из (3) следует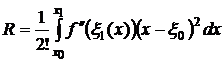 
.
Т. к. второй множитель подынтегрального выражения не меняет знак, то по теореме о среднем получим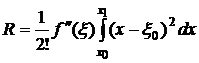 
, где 
. После интегрирования получим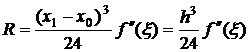 
. (4)
Сравнивая с остаточным членом формулы трапеций, мы видим, что погрешность формулы прямоугольников в два раза меньше, чем погрешность формулы трапеций. Этот результат верен, если в формуле прямоугольников мы берём значение функции в средней точке.
Получим формулу прямоугольников и остаточный член для интервала [a, b]. Пусть задана сетка xi=a+ih, i=0,1,...,n, h=xi+1-xi
. Рассмотрим сетку εi=ε0+ih, i=1,2,..,n, ε0=a-h/2. Тогда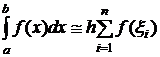 
. (5)
Остаточный член 
.
Геометрически формула прямоугольников может быть представлена следующим рисунком:
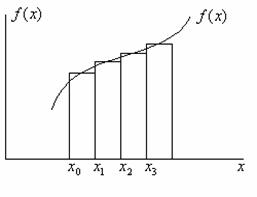
Если функция f(x) задана таблично, то используют либо левостороннюю формулу прямоугольников (для равномерной сетки)
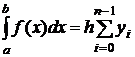
либо правостороннюю формулу прямоугольников
.
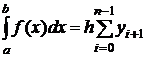Погрешность этих формул оценивается через первую производную. Для интервала [x0, x1] погрешность равна
; 
.
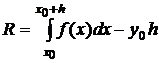После интегрирования получим .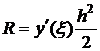
Пример. Вычислить интеграл 
при n=5:
а) по формуле трапеций;
б) по формуле прямоугольников;
в) по формуле Симпсона;
г) по формуле Гаусса;
д) по формуле Чебышева.
Рассчитать погрешность.
Решение. Для 5-ти узлов интегрирования шаг сетки составит 0.125.
При решении будем пользоваться таблицей значений функции. Здесь f(x)=1/x.
| x | f(x) | ||
| x0 | 0.5 | y0 | 2 |
| x1 | 0.625 | y1 | 1.6 |
| x2 | 0.750 | y2 | 1.33 |
| x3 | 0.875 | y3 | 1.14 |
| x4 | 1.0 | y4 | 1 |
I=h/2×[y0+2(y1+y2+y3)+y4];
I=(0.125/2)×[2+2(1.6+1.33+1.14)+1]=0.696;
R= [-(b-a)/12]×h×y¢¢(x);
f¢¢(x)=2/(x3).
Максимальное значение второй производной функции на интервале [0,5;1] равно 16: max {f¢¢(x)}, xÎ[0.5,1]=2/(0.53)=16, поэтому
R=[-(1-0.5)/12]×0.125×16=-0.0833;
б) формула прямоугольников:
для левосторонней формулы I=h×(y0+y1+y2+y3);
I=0.125×(2+1.6+1.33+1.14)=0.759;
R=[(b-a)/6]×h2×y¢¢(x);
R=[(1-0.5)/6]×0.1252×16=0.02;
в) формула Симпсона:
I=(2h/6)×{y0+y4+4×(y1+y3)+2×y2};
I=(2×0.125)/6×{2+1+4×(1.6+1.14)+2×1.33}=0.693;
R=[-(b-a)/180]×h4×y(4)(x);
f(4)(x)=24/(x5)=768;
R=[-(1-0.5)/180]×(0.125)4×768=-5.2e-4;
г) формула Гаусса:
I=(b-a)/2×[A1×f(x1)+ A2×f(x2)+ A3×f(x3)+ A4×f(x4)+ A5×f(x5)];
xi =(b+a)/2+ti (b-a)/2
(Ai , ti - табличные значения).
| t (n=5) | A (n=5) | ||||||
| x1 | 0.9765 | y1 | 1.02 | t1 | 0.90617985 | A1 | 0.23692688 |
| x2 | 0.8846 | y2 | 1.13 | t2 | 0.53846931 | A2 | 0.47862868 |
| x3 | 0.75 | y3 | 1.33 | t3 | 0 | A3 | 0.56888889 |
| x4 | 0.61 | y4 | 1.625 | t4 | -0.53846931 | A4 | 0.47862868 |
| x5 | 0.52 | y5 | 1.91 | t5 | -0.90617985 | A5 | 0.23692688 |
д) формула Чебышева:
I=[(b-a)/n] ×S f(xi), i=1..n,
xi=(b+a)/2+[ ti (b-a)]/2 - необходимое приведение интервала интегрирования к интервалу [-1;1].
Для n=5
| t1 | 0.832498 |
| t2 | 0.374541 |
| t3 | 0 |
| t4 | -0.374541 |
| t5 | -0.832498 |
| x1 | 0,958 | f(x1) | 1,043 |
| x2 | 0,844 | f(x2) | 1,185 |
| x3 | 0,75 | f(x3) | 1,333 |
| x4 | 0,656 | f(x4) | 1,524 |
| x5 | 0,542 | f(x5) | 1,845 |
I=(1-0,5)/5×6,927=0,6927.
