Правило треугольников
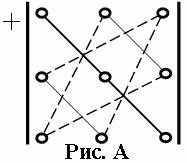
 Три слагаемых, входящих в сумму B со знаком «плюс», находятся следующим образом: одно слагаемое состоит из произведения элементов, расположенных на главной диагонали, два других – произведения элементов, лежащих на параллели к этой диагонали с добавлением третьего множителя из противоположного угла. (Получается два треугольника, вершинами которых являются перемножаемые элементы.) (рис. А).
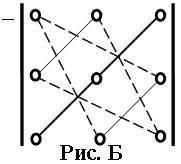
Слагаемые, входящие в B со знаком «минус», строятся таким же образом относительно побочной диагонали. (рис. Б).
Три слагаемых, входящих в сумму B со знаком «плюс», находятся следующим образом: одно слагаемое состоит из произведения элементов, расположенных на главной диагонали, два других – произведения элементов, лежащих на параллели к этой диагонали с добавлением третьего множителя из противоположного угла. (Получается два треугольника, вершинами которых являются перемножаемые элементы.) (рис. А).
Слагаемые, входящие в B со знаком «минус», строятся таким же образом относительно побочной диагонали. (рис. Б).
Инструкция для нахождения определителя методом треугольников (методом Саррюса). Заполните матрицу, нажмите Далее. Полученное решение сохраняется в файле Word. Дополнительно создается шаблон решения в Excel.
Пример. Найти определитель методом Саррюса.
| = 1•(-2)•(-2) - 1•4•1 - 0•5•(-2) + 0•4•1 + 3•5•4 - 3•4•(-2) = 84 |
Примечание. Определитель матрицы можно найти и другими способами, а именно:
- вычисление определителя методом Гаусса.
- вычисление определителя через алгебраические дополнения (разложением по элементам первой строки).
- вычисление определителя методом декомпозиции.
Пример. Вычислить определитель 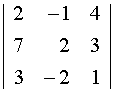 двумя способами:
двумя способами:
а) разложением по элементам первой строки, б) по правилу Саррюса.
а) 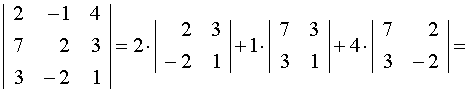
=2·(2·1-3·(-2)) + 1·(7·1-3·3) + 4(7·(-2)-3·2) = -66
б) 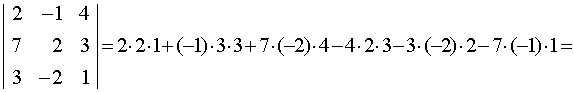 <
<
= 4 – 9 – 56 – 24 + 12 + 7 = -66