Определители второго и третьего порядков

, (*)

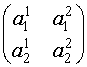Пары элементов a₁¹, a₁² и a₂¹, a₂² образуют строки матрицы, а пары a₁¹, a₂¹ и a₁², a₂² – столбцы.

Число (a₁¹·a₂² - a₁²·a₂¹), составленное из элементов матрицы (*), называют определителем второго порядка и обозначают 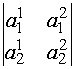. Таким образом, чтобы сосчитать определитель второго порядка, надо перемножить элементы, стоящие на главной диагонали и вычесть произведение элементов, стоящих на побочной диагонали, например, определитель матрицы  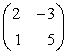равен .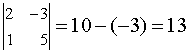

Матрицей третьего порядка называется таблица, составленная из девяти элементов

: .

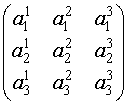Матрица, имеющая одинаковое число строк и столбцов, называется квадратной, а число ее строк (столбцов) называется порядком матрицы.

Говорят, что элементы a₁¹, a₂², a₃³ образуют главную диагональ, а a₁³, a₂², a₃¹ – побочную.

Определителем третьего порядка  называется число, равное сумме 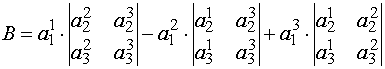. Это выражение называется разложением определителя по элементам первой строки.

см. также методы вычисления определителей 4-го порядка