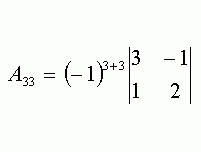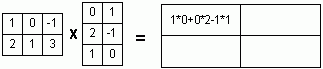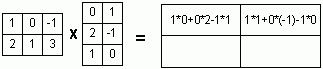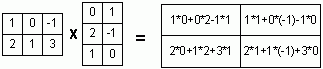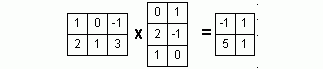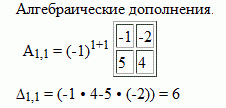Общее решение (О.Р.) и Ф.С.Р. однородной СЛАУ
Пример. Решить СЛАУ методом Гаусса: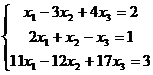 .
.
Первый метод решения. Запишем систему в виде расширенной матрицы:
|
|
|
|
|
|
|
|
x2 = [5 - ( - 45x3)]/35
x1 = [3 - ( - 12x2 + 17x3)]/11
Необходимо переменную x3 принять в качестве свободной переменной и через нее выразить остальные переменные.
Приравняем переменную x3 к 0
Из 2-ой строки выражаем x2
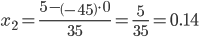
Из 3-ой строки выражаем x1
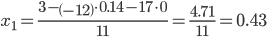
Частное решение системы: (0.43; 0.14; 0).
Второй метод решения. Запишем систему в виде расширенной матрицы:
|
|
|
|
Умножим 2-ую строку на (k = -1 / 2 = -1/2) и добавим к 3-ой:
| 11 | -12 | 17 | 3 |
| 2 | 1 | -1 | 1 |
| 0 | -7/2 | 9/2 | 3/2 |
| 11 | -12 | 17 | 3 |
| 0 | 35/11 | -45/11 | 5/11 |
| 0 | -7/2 | 9/2 | 3/2 |
Умножим 2-ую строку на (k = 7/2 / 35/11 = 11/10) и добавим к 3-ой:
| 11 | -12 | 17 | 3 |
| 0 | 35/11 | -45/11 | 5/11 |
| 0 | 0 | 0 | 2 |
|
|
x1 = 3/11 - ( - 12/11x2 + 17/11x3)
x2 = 1/7 - ( - 9/7x3)
3-ая строка является линейной комбинацией других строк.
Необходимо переменную x3 принять в качестве свободной переменной и через нее выразить остальные переменные.
Приравняем переменную x3 к 0
Из 2-ой строки выражаем x2
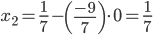
Из 1-ой строки выражаем x1
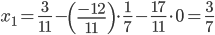
7. Найти О.Р. (общее решение) и Ф.С.Р. однородной СЛАУ:
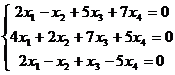 .
.
Выпишем основную матрицу системы:
|
Умножим 1-ую строку на (2). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:
|
|
|
|
Этот минор является базисным. В него вошли коэффициенты при неизвестных x1,x2,x3, значит, неизвестные x1,x2,x3 – зависимые (базисные), а x4 – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.
|
8x3 = - 24x4
4x2 + 5x3 = - 15x4
2x1 - x2 + x3 = 5x4
Методом исключения неизвестных находим нетривиальное решение:
Получили соотношения, выражающие зависимые переменные x1,x2,x3 через свободные x4, то есть нашли общее решение:
x3 = - 3x4
x2 = 0
x1 = 4x4
8. Найти О.Р. (общее решение) неоднородной СЛАУ:
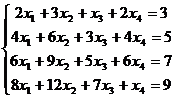 .
.
Решение. Исследуем эту систему по теореме Кронекера-Капелли. Выпишем расширенную и основную матрицы:
|
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Умножим 1-ую строку на (2). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:
|
| 0 | -1 | 0 | 1 | 0 |
| 6 | 3 | 4 | 5 | -4 |
| 9 | 5 | 6 | 7 | -6 |
| 12 | 7 | 1 | 9 | -8 |
| x2 | x3 | x4 | x1 |
|
|
|
|
Этот минор является базисным. В него вошли коэффициенты при неизвестных x2,x3,x4, значит, неизвестные x2,x3,x4 – зависимые (базисные), а x1 – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.
|
- 63x4 = 0
- 3x3 + 63x4 = 3
12x2 + 7x3 + x4 = 9 - 8x1
Методом исключения неизвестных находим:
Получили соотношения, выражающие зависимые переменные x2,x3,x4 через свободные x1, то есть нашли общее решение:
x4 = 0
x3 = - 1
x2 = 1.33 - 0.67x1
Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Система является неопределенной, т.к. имеет более одного решения.
Пример. Найти собственные числа и собственные векторы матрицы
![]() .
.
Решение. Исходная матрица имеет вид:
|
(2-λ)x1-2x2 = 0
6x1 + (-5-λ)x2 = 0
Составляем характеристическое уравнение и решаем его.
|
((2-λ)•(-5-λ)-6•(-2)) = 0
После преобразований, получаем:
λ2 +3λ + 2 = 0
D = 32 - 4 • 1 • 2 = 1
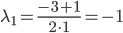
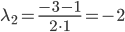
3x1-2y1 = 0
6x1-4y1 = 0
Собственный вектор, отвечающий числу λ1 = -1 при x1 = 2:
x1=(2;3)
В качестве единичного собственного вектора принимаем вектор:
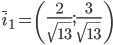
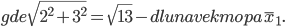
или
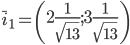
Координаты второго собственного вектора, соответствующего второму собственному числу λ2 = -2, находим из системы:
4x1-2y1 = 0
6x1-3y1 = 0
x2=(1;2)
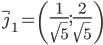
или
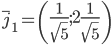
Пример. Задана матрица A линейного преобразования в некотором базисе ![]() ,
, ![]() ,
, ![]() . Найдите матрицу этого преобразования в базисе
. Найдите матрицу этого преобразования в базисе ![]() ,
, ![]() ,
, ![]() , если :
, если :
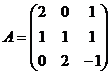 ,
,
![]()
![]()
![]()