Корреляционный анализ в EXCEL

Формула для вычислений	Функция EXCEL или инструмент Анализа данных	Результат вычислений
Коэффициент корреляции	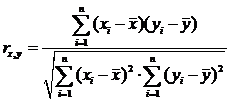КОРРЕЛ(массив1;массив2) Массив1 — это ячейка интервала значений. Массив2 — это второй интервал ячеек со значениями	Возвращает коэффициент корреляции меду интервалами ячеек массив1 и массив2.
Оценка значимости коэффициента парной корреляции с использованием t - критерия Стьюдента. 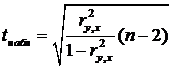Вычисленное по этой формуле значение tнаблсравнивается с критическим значением t-критерия, которое берется из таблицы значений t Стьюдента с учетом заданного уровня значимости и числа степеней свободы (n-2).	СТЬЮДРАСПОБР (вероятность; степени_свободы) Вероятность — вероятность, соответствующая двустороннему распределению Стьюдента. Степени_свободы — число степеней свободы, характеризующее распределение.	Возвращает t-значение распределения Стьюдента как функцию вероятности и числа степеней свободы.
Матрица коэффициентов парной корреляции	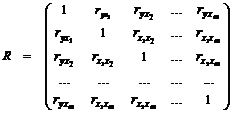Обращение к средствам анализа данных. Они доступны через команду Анализ данныхменю Сервис. Для вычисления матрицы коэффициентов парной корреляции R следует воспользоваться инструментом Корреляция.	Инструмент Корреляция применяется, если имеется более двух переменных измерений для каждого объекта. В результате выдается таблица, корреляционная матрица, показывающая значение функции КОРРЕЛ для каждой возможной пары переменных измерений. Любое значение коэффициента корреляции должно находиться в диапазоне от -1 до +1 включительно.

см. также Регрессионный анализ в Excel