Проверка на гетероскедастичность при помощи теста ранговой корреляции Спирмена

Пример решен с помощью калькулятора.

Решение
Видео решение

Система нормальных уравнений:
a•n + b∑x = ∑y
a∑x + b∑x² = ∑y•x
Для наших данных система уравнений имеет вид
40a + 2368 b = 653.1
2368 a + 155959.7 b = 41138.21
Из первого уравнения выражаем а и подставим во второе уравнение:
Получаем эмпирические коэффициенты регрессии: b = 0.16, a = 7.04
Уравнение регрессии (эмпирическое уравнение регрессии):
y = 0.16 x + 7.04
Эмпирические коэффициенты регрессии a и b являются лишь оценками теоретических коэффициентов β_i, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных.

Для расчета параметров линейной регрессии построим расчетную таблицу (табл.)

x	y	x²	y²	x • y	y(x)	(y_i-y_cp)²	(y-y(x))²	(x_i-x_cp)²	\|y - y_x\|:y
25.5	14.5	650.25	210.25	369.75	11.04	3.34	11.97	1135.69	0.24
26.5	11.3	702.25	127.69	299.45	11.2	25.28	0.0105	1069.29	0.00908
27.2	14.7	739.84	216.09	399.84	11.31	2.65	11.51	1024	0.23
29.6	10.2	876.16	104.04	301.92	11.68	37.55	2.2	876.16	0.15
35.7	13.5	1274.49	182.25	481.95	12.64	7.99	0.74	552.25	0.0636
38.6	9.9	1489.96	98.01	382.14	13.1	41.31	10.21	424.36	0.32
39	12.4	1521	153.76	483.6	13.16	15.43	0.58	408.04	0.0612
39.3	8.6	1544.49	73.96	337.98	13.21	59.71	21.21	396.01	0.54
40	10.3	1600	106.09	412	13.32	36.33	9.09	368.64	0.29
41.9	13.9	1755.61	193.21	582.41	13.61	5.89	0.0821	299.29	0.0206
42.5	14.9	1806.25	222.01	633.25	13.71	2.04	1.42	278.89	0.08
44.2	11.6	1953.64	134.56	512.72	13.97	22.35	5.64	225	0.2
44.8	21.5	2007.04	462.25	963.2	14.07	26.75	55.23	207.36	0.35
45.5	10.8	2070.25	116.64	491.4	14.18	30.55	11.41	187.69	0.31
45.5	13.8	2070.25	190.44	627.9	14.18	6.39	0.14	187.69	0.0274
48.3	16	2332.89	256	772.8	14.62	0.11	1.91	118.81	0.0864
49.5	18.2	2450.25	331.24	900.9	14.81	3.51	11.52	94.09	0.19
52.3	19.1	2735.29	364.81	998.93	15.25	7.69	14.86	47.61	0.2
55.7	16.3	3102.49	265.69	907.91	15.78	0.000756	0.27	12.25	0.032
59	17.5	3481	306.25	1032.5	16.3	1.37	1.45	0.04	0.0688
61	10.9	3721	118.81	664.9	16.61	29.46	32.6	3.24	0.52
61.7	16.1	3806.89	259.21	993.37	16.72	0.0518	0.38	6.25	0.0385
62.5	10.5	3906.25	110.25	656.25	16.85	33.96	40.26	10.89	0.6
64.7	10.6	4186.09	112.36	685.82	17.19	32.8	43.43	30.25	0.62
69.7	29	4858.09	841	2021.3	17.97	160.59	121.56	110.25	0.38
71.2	8.2	5069.44	67.24	583.84	18.21	66.06	100.2	144	1.22
73.8	14.3	5446.44	204.49	1055.34	18.62	4.11	18.65	213.16	0.3
74.7	21.8	5580.09	475.24	1628.46	18.76	29.95	9.25	240.25	0.14
75.8	26.1	5745.64	681.21	1978.38	18.93	95.5	51.38	275.56	0.27
76.9	20	5913.61	400	1538	19.1	13.49	0.8	313.29	0.0448
79.2	19.8	6272.64	392.04	1568.16	19.47	12.06	0.11	400	0.0169
81.5	21.2	6642.25	449.44	1727.8	19.83	23.74	1.89	497.29	0.0648
82.4	29	6789.76	841	2389.6	19.97	160.59	81.59	538.24	0.31
82.8	17.3	6855.84	299.29	1432.44	20.03	0.95	7.45	556.96	0.16
83	23.5	6889	552.25	1950.5	20.06	51.44	11.82	566.44	0.15
85.9	22	7378.81	484	1889.8	20.52	32.18	2.2	712.89	0.0674
86.4	18.3	7464.96	334.89	1581.12	20.59	3.89	5.27	739.84	0.13
86.9	13.7	7551.61	187.69	1190.53	20.67	6.9	48.62	767.29	0.51
88.3	14.5	7796.89	210.25	1280.35	20.89	3.34	40.87	846.81	0.44
89	27.3	7921	745.29	2429.7	21	120.4	39.66	888.04	0.23
2368	653.1	155959.7	11881.19	41138.21	653.1	1217.7	829.46	15774.1	9.69

Проверка наличия гетероскедастичности.
1) Методом графического анализа остатков.
В этом случае по оси абсцисс откладываются значения объясняющей переменной X, а по оси ординат либо отклонения e_i, либо их квадраты e²_i.
Если имеется определенная связь между отклонениями, то гетероскедастичность имеет место. Отсутствие зависимости скорее всего будет свидетельствовать об отсутствии гетероскедастичности.
2) При помощи теста ранговой корреляции Спирмена.
Коэффициент ранговой корреляции Спирмена.
Присвоим ранги признаку e_i и фактору X. Найдем сумму разности квадратов d².
По формуле вычислим коэффициент ранговой корреляции Спирмена.
$p = 1 - 6{sum{}{}{}d^{2}}/{n^{3}-n}$
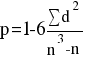
Если среди значений признаков х и у встречается несколько одинаковых, образуются связанные ранги, т. е. одинаковые средние номера; например, вместо одинаковых по порядку третьего и четвертого значений признака будут два ранга по 3,5. В таком случае коэффициент Спирмена вычисляется как:
$p = 1 - 6{sum{}{}{}d^{2} - A - B}/{sqrt{(n^{3}-n-12A)(n^{3}-n-12B)}}$
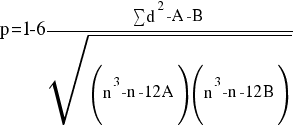
где
$A = {1}/{12}sum{}{}{}(A^{3}_{j} - A_{j})$
$B = {1}/{12}sum{}{}{}(B^{3}_{k} - B_{k})$
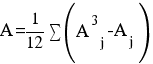
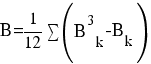
j - номера связок по порядку для признака х;
А_j - число одинаковых рангов в j-й связке по х;
k - номера связок по порядку для признака у;
В_k - число одинаковых рангов в k-й связке по у.

X	e_i	ранг X, d_x	ранг e_i, d_y	(d_x - d_y)²
25.5	3.46	1	26	625
26.5	0.1	2	1	1
27.2	3.39	3	23	400
29.6	1.48	4	15	121
35.7	0.86	5	8	9
38.6	3.2	6	21	225
39	0.76	7	7	0
39.3	4.61	8	29	441
40	3.02	9	19	100
41.9	0.29	10	2	64
42.5	1.19	11	10	1
44.2	2.37	12	17	25
44.8	7.43	13	37	576
45.5	3.38	14.5	22	56.25
45.5	0.38	14.5	4	110.25
48.3	1.38	16	13	9
49.5	3.39	17	24	49
52.3	3.85	18	27	81
55.7	0.52	19	5	196
59	1.2	20	11	81
61	5.71	21	30	81
61.7	0.62	22	6	256
62.5	6.35	23	32	81
64.7	6.59	24	34	100
69.7	11.03	25	40	225
71.2	10.01	26	39	169
73.8	4.32	27	28	1
74.7	3.04	28	20	64
75.8	7.17	29	36	49
76.9	0.9	30	9	441
79.2	0.33	31	3	784
81.5	1.37	32	12	400
82.4	9.03	33	38	25
82.8	2.73	34	18	256
83	3.44	35	25	100
85.9	1.48	36	14	484
86.4	2.29	37	16	441
86.9	6.97	38	35	9
88.3	6.39	39	33	36
89	6.3	40	31	81
				7253.5

A = 6/12 = 0.5
B = 0/12 = 0

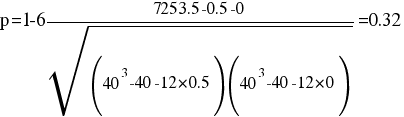
$p = 1 - 6{7253.5-0.5-0}/{sqrt{(40^{3} - 40-12 mul 0.5)(40^{3} - 40-12 mul 0)}} = 0.32$

Связь между признаком e_i и фактором X слабая и прямая
Оценка коэффициента ранговой корреляции Спирмена.
Значимость коэффициента ранговой корреляции Спирмена

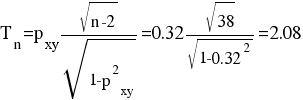
$T_{n} = p_{xy} {sqrt{n-2}}/{sqrt{1 - p^{2}_{xy}}} = 0.32 {sqrt{38}}/{sqrt{1 - 0.32^{2}}} = 2.08$

По таблице Стьюдента находим t_табл:
t_табл(n-m-1;α/2) = (38;0.05/2) = 2.021
Поскольку Tнабл > tтабл, то отклоняем гипотезу о равенстве 0 коэффициента ранговой корреляции. Другими словами, коэффициент ранговой корреляции статистически - значим.
Проверим гипотезу H₀: гетероскедастичность отсутствует. Поскольку 2.021 < 2.08, то гипотеза об отсутствии гетероскедастичности отвергается.

Проверка на гетероскедастичность при помощи теста ранговой корреляции Спирмена

Правила ввода данных

Поиск

Процесс

Сообщение