Доверительный интервал для математического ожидания
Рассмотрим вначале случай, когда выборка объема n извлечена из нормальной генеральной совокупности X~N(a, σ) с неизвестным параметром a и известным σ. Параметр a является математическим ожиданием (генеральным средним) случайной величины Х. В качестве точечной оценки параметра a возьмем выборочное среднее:
. Для уточнения приближенного равенства a ≈ x построим доверительный интервал, накрывающий параметр a с заданной доверительной вероятностью γ.
Если выборка объема n извлекается из нормальной генеральной совокупности N(a,σ), то статистика
имеет нормальное распределение с параметрами: 
. Поэтому доверительная вероятность γ удовлетворяет соотношению:
(2)
отсюда
(3)Значение uкр найдем с помощью таблицы функции Лапласа, учитывая, что Ф(uкр)=γ/2
(4)
1-α - доверительный интервал
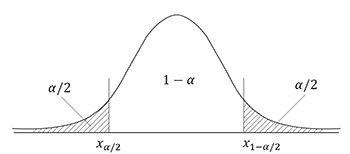
Двусторонняя критическая область
Этот метод построения доверительного интервала применяется и в случае, если генеральная совокупность Х не является нормальной. Согласно центральной предельной теореме, для выборки достаточно большого объема выборочное среднее X будет иметь приближенно нормальное распределение с параметрами M(X)=a и
где a и σ — соответствующие параметры генеральной совокупности. В этом случае для построения доверительного интервала используют формулу (4), определяя значение uкр по таблицам функции Лапласа, если n>30. При n≤30 значение uкр заменяют на tкр, которое определяют по таблице распределения Стьюдента, и формула (4) принимает вид:
(5)где tкр = t(k;α), k=n-1, α=1-γ (область двусторонняя).
Если значение параметра σ неизвестно, то доверительный интервал строят по формуле (5), заменяя параметр σ с его оценкой
Величина
называется средней ошибкой выборки и зависит от способа отбора: в случае конечной генеральной совокупности объема N вносится «поправка на бесповторность отбора», равная 
(табл. 1).
Таблица 1 - Средняя ошибка выборки для генерального среднего
| Генеральная совокупность | Бесконечная | Конечная объема N |
| Тип отбора | Повторный | Бесповторный |
| Средняя ошибка выборки |
| 
|
Пример №1. Служба контроля Энергосбыта провела выборочную проверку расхода электроэнергии жителями одного из многоквартирных домов. С помощью случайного отбора было выбрано 10 квартир и определен расход электроэнергии в течение одного из летних месяцев (кВт*час): 125, 78, 102, 140, 90, 45, 50, 125, 115, 112.
С вероятностью 0.95 определите доверительный интервал для среднего расхода электроэнергии на одну квартиру во всем доме при условии, что отбор был: а) повторным; б) бесповторным, и в доме имеется 70 квартир.
Решение. По условию задачи объем выборки n=10, т.е. выборка малая. В случае повторного отбора найдем границы доверительного интервала для генерального среднего по формуле (5), считая σ≈s:
Найдем выборочное среднее арифметическое:
+(102-98.2)2+(140-98.2)2+(90-98.2)2+(45-98.2)2 + (50-98.2)2+(125-98.2)2+(115-98.2)2+(112-98.2)2 = 1033.29
Тогда оценка среднего квадратического отклонения σ равна
По таблице распределения Стьюдента найдем значение tкр=t(k; α) для двусторонней критической области. Число степеней свободы k здесь равно k=n-1=9, а вероятность α=1-γ=0,05. Тогда tкр=t(k; α) = 2.26 (двусторонняя область).
При повторном случайном отборе средняя ошибка выборки равна
а предельная ошибка 
т.е. доверительный интервал имеет границы (x-ε; x+ε) = (98.2 - 22.97; 98.2 + 22.97) = (75.63; 121.17)
При условии, что отбор квартир был повторным, с вероятностью 0.95 можно ожидать, что средний расход электроэнергии на одну квартиру во всем доме находится в интервале от 75.63 (кВт*час) до 121.17 (кВт*час).
Найдем теперь границы доверительного интервала, считая отбор бесповторным. Предельную ошибку ε определим с учетом того, что генеральная совокупность конечна и имеет объем N (табл. 1).
Из условия задачи x=98.2, s=32.14, n=10, N=70, γ=0.95, tкр= tкр(9; 0.05) = 2.26. Отсюда предельная ошибка выборки
и доверительный интервал имеет границы (x-ε; x+ε) = (98.2-21.27; 98.2+21.27) = (76.93; 119.47)
При условии, что отбор квартир был бесповторным, с вероятностью 0.95 можно утверждать, что средний расход электроэнергии на одну квартиру во всем доме находится в интервале от 76.93 (кВт*час) до 119.47 (кВт*час).
Формула (3) позволяет при заданной доверительной вероятности γ и требуемой точности ε определить объем выборки n, учитывая тип отбора данных.
Пример №2. С помощью случайного повторного отбора определяется средний стаж работы служащих фирмы. Предполагается, что он подчиняется нормальному закону распределения. Каким должен быть объем выборки, чтобы с доверительной вероятностью 0.95 можно было утверждать, что, принимая полученный средний стаж работы за истинный, совершается погрешность, не превышающая 0.5 года, если стандартное отклонение σ равно 2.7 года?
Решение. По условию ε=0.5, σ=2.7, γ =0.95 и требуется найти объём выборки n при повторном отборе. В этом случае 2Ф(uкр)= γ, где 
По таблице функции Лапласа найдем, при каком uкр значение Ф(uкр)=γ/2=0.475. Получим uкр=1.96. Отсюда необходимый объем выборки
Учитывая, что необходимо не превышать заданную ошибку, округляем результат до большего целого: n=113.
Итак, чтобы с вероятностью 0.95 и точностью ε=0.5 года определить средний стаж работы в фирме, требуется опросить не менее 113 служащих.
Пример. В результате 10 независимых измерений некоторой величины Х, выполненных с одинаковой точностью, получены опытные данные, приведенные в таблице. Предполагая, что результаты измерений подчинены нормальному закону распределения вероятностей, оценить истинное значение величины Х при помощи доверительного интервала, покрывающего истинное значение величины Х с доверительной вероятностью 0,95.
| 1,2 | 2,3 | 2,7 | 2,1 | 2,6 | 3,1 | 1,8 | 3,0 | 1,7 | 1,4 |
Проранжируем ряд. Для этого сортируем его значения по возрастанию.
| x | (x - xср)2 |
| 1.2 | 0.98 |
| 1.4 | 0.62 |
| 1.7 | 0.24 |
| 1.8 | 0.15 |
| 2.1 | 0.0081 |
| 2.3 | 0.0121 |
| 2.6 | 0.17 |
| 2.7 | 0.26 |
| 3 | 0.66 |
| 3.1 | 0.83 |
| 21.9 | 3.93 |
Простая средняя арифметическая (математическое ожидание)
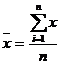
Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).
Несмещенная оценка дисперсии - состоятельная оценка дисперсии.
Среднее квадратическое отклонение.
Каждое значение ряда отличается от среднего значения 2.19 не более, чем на 0.63
Оценка среднеквадратического отклонения.
Доверительный интервал для генерального среднего.
Поскольку n ≤ 30, то определяем значение tkp по таблице распределения Стьюдента.
По таблице Стьюдента находим Tтабл
Tтабл (n-1;α/2) = (9;0.025) = 2.262
(2.19 - 0.47;2.19 + 0.47) = (1.72;2.66)
С вероятностью 0.95 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала.
Пример. Если исходные данные необходимо предварительно сгруппировать, то решение можно найти с помощью сервиса группировка данных
. Число групп приближенно определяется по формуле Стэрджесса
n = 1 + 3,2log n = 1 + 3,2log 100 = 8
Тогда ширина интервала составит:
| Группы | x | Кол-во f | x·f | S | (x - x)·f | (x - x)2·f | (x - x)3·f | (x - x)4·f | Частота |
| 16.56 - 23.12 | 19.84 | 4 | 79.36 | 4 | 111 | 3079.98 | -85465.85 | 2371574.75 | 0.04 |
| 23.12 - 29.68 | 26.4 | 1 | 26.4 | 5 | 21.19 | 448.97 | -9513.03 | 201569.79 | 0.01 |
| 29.68 - 36.24 | 32.96 | 9 | 296.64 | 14 | 131.66 | 1926.02 | -28175.3 | 412170.89 | 0.09 |
| 36.24 - 42.8 | 39.52 | 15 | 592.8 | 29 | 121.03 | 976.58 | -7879.85 | 63580.96 | 0.15 |
| 42.8 - 49.36 | 46.08 | 23 | 1059.84 | 52 | 34.7 | 52.36 | -79 | 119.19 | 0.23 |
| 49.36 - 55.92 | 52.64 | 26 | 1368.64 | 78 | 131.33 | 663.38 | 3350.87 | 16925.89 | 0.26 |
| 55.92 - 62.48 | 59.2 | 17 | 1006.4 | 95 | 197.39 | 2291.94 | 26612.17 | 308999.19 | 0.17 |
| 62.48 - 69.04 | 65.76 | 5 | 328.8 | 100 | 90.86 | 1650.96 | 29999.97 | 545135.47 | 0.05 |
| 100 | 4758.88 | 0 | 839.16 | 11090.19 | -71150.04 | 3920076.14 | 1 |
Средняя взвешенная
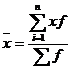
Мода
Выбираем в качестве начала интервала 49.36, так как именно на этот интервал приходится наибольшее количество
Наиболее часто встречающееся значение ряда – 51
Медиана
Медиана делит выборку на две части: половина вариант меньше медианы, половина — больше
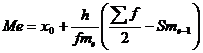
Таким образом, 50% единиц совокупности будут меньше по величине 48.79
Квартили
Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине Q1; 25% будут заключены между Q1 и Q2; 25% - между Q2 и Q3; остальные 25% превосходят Q3
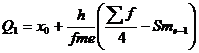
Таким образом, 25% единиц совокупности будут меньше по величине 41.05
Q2 совпадает с медианой, Q2 = 48.79
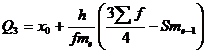
Остальные 25% превосходят значение 55.16.
Квартильный коэффициент дифференциации.
k = Q1 / Q3 = 41.05 / 55.16 = 0.74
Децили (децентили)
Децили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 10% единиц совокупности будут меньше по величине D1; 80% будут заключены между D1 и D9; остальные 10% превосходят D9
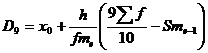
Таким образом, 10% единиц совокупности будут меньше по величине 33.32
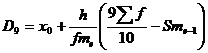
Остальные 10% превосходят 60.55
Показатели вариации.
Размах вариации
R = Xmax - Xmin = 69.02 - 16.56 = 52.46
Среднее линейное отклонение
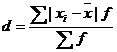
Каждое значение ряда отличается от другого не более, чем на 8.39
Дисперсия
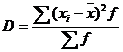
Несмещенная оценка дисперсии.
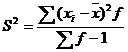
Среднее квадратическое отклонение.
Каждое значение ряда отличается от среднего значения 47.59 не более, чем на 10.53
Оценка среднеквадратического отклонения.
Коэффициент вариации
Поскольку v<30%, то совокупность однородна, а вариация слабая. Полученным результатам можно доверять.
Показатели формы распределения.
Коэффициент осцилляции
Относительное линейное отклонение
Относительный показатель квартильной вариации
Степень асимметрии
Симметричным является распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой.
Отрицательный знак свидетельствует о наличии левосторонней асимметрии
Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения.
Ex > 0 - островершинное распределение
Расчет доверительного интервала для генеральной средней
Доверительный интервал для генерального среднего - это интервал изменений среднего значения совокупности, в пределах которого с заданной вероятностью будет находиться выборочное среднее при выборке данных большего размера.
Поскольку n>30, то определяем значение tkp по таблицам функции Лапласа
В этом случае 2Ф(tkp) = 1 - γ
Ф(tkp) = (1 - γ)/2 = 0.95/2 = 0.475
По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0.475
tkp (γ) = (0.475) = 1.96
(47.59 - 2.07;47.59 + 2.07) = (45.5188;49.6588)
С вероятностью 0.95 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала.
