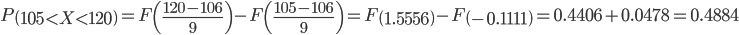Вероятность попадания в интервал
Пример №1. Для случайной величины X, распределенной по нормальному закону с параметрами mx=17,1 и σ=2,4 определить вероятность попадания в интервал [16; 19].Решение получаем с помощью сервиса Доверительный интервал
. Вероятность попадания величины X в заданный интервал (α ; β).
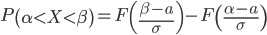
где Ф(x) — функция Лапласа
Учитывая, что функция Лапласа нечетная, т.е. Ф(-x) = -Ф(x), получим:
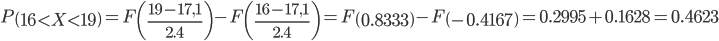
Пример №2. Функция распределения CB X имеет вид:

Найти вероятность того, что случайная величина окажется в интервале (3,6). (см. свойства F (x)).
Решение:
P(3 < x < 6) = F(6) – F(3) = F(x>5) – F(3) = 1 – 32/26 = 1 – 9/26 = 17/26
Пример №3. Средний процент выполнения плана некоторыми предприятиями составляет 106%, среднее квадратическое отклонение 9%. Полагая, что выполнение плана этой группой предприятий подчиняется нормальному закону, определить процент предприятий, не выполняющих план.
Решить задачу при условии, что требуется определить процент предприятий, выполняющих план от 105% до 120%.
Решение:
а) Чтобы определить процент предприятий, не выполняющих план, необходимо найти P(X < 106) = 1 - Ф(105/9) = 0.5.
б) Здесь a = 106, α=105, β = 120, σ = 9.