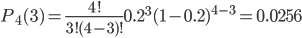Испытания по схеме Бернулли
Производится n опытов по схеме Бернулли с вероятностью успеха p. Пусть X - число успехов. Случайная величина X имеет область значений {0,1,2,...,n}. Вероятности этих значений можно найти по формуле:
, где Cmn - число сочетаний из n по m. 
Ряд распределения имеет вид:
| x | 0 | 1 | ... | m | n |
| p | (1-p)n | np(1-p)n-1 | ... | Cmnpm(1-p)n-m | pn |
Назначение сервиса. Онлайн-калькулятор используется для построения биноминальным ряда распределения и вычисления всех характеристик ряда: математического ожидания, дисперсии и среднеквадратического отклонения. Отчет с решением оформляется в формате Word.
Числовые характеристики случайной величины, распределенной по биноминальному закону
Математическое ожидание случайной величины Х, распределенной по биноминальному закону.M[X]=np
Дисперсия случайной величины Х, распределенной по биноминальному закону.
D[X]=npq
Пример №1. Изделие может оказаться дефектным с вероятностью р = 0.3 каждое. Из партии выбирают три изделия. Х – число дефектных деталей среди отобранных. Найти (все ответы вводить в виде десятичных дробей): а) ряд распределения Х; б) функцию распределения F(x).
Решение. Случайная величина X имеет область значений {0,1,2,3}.
Найдем ряд распределения X.
P3(0) = (1-p)n = (1-0.3)3 = 0.34
P3(1) = np(1-p)n-1 = 3(1-0.3)3-1 = 0.44
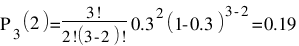
| xi | 0 | 1 | 2 | 3 |
| pi | 0.34 | 0.44 | 0.19 | 0.027 |
Математическое ожидание находим по формуле M[X]= np = 3*0.3 = 0.9
Проверка: m = ∑xipi.
Математическое ожидание M[X].
M[x] = 0*0.34 + 1*0.44 + 2*0.19 + 3*0.027 = 0.9
Дисперсию находим по формуле D[X]=npq = 3*0.3*(1-0.3) = 0.63
Проверка: d = ∑x2ipi - M[x]2.
Дисперсия D[X].
D[X] = 02*0.34 + 12*0.44 + 22*0.19 + 32*0.027 - 0.92 = 0.63
Среднее квадратическое отклонение σ(x).
![sigma(x) = sqrt{D[X]} = sqrt{0.63} = 0.79](https://www.semestr.ru/images/math/math/3_tests-bernoulli.png "sigma(x) = sqrt{D[X]} = sqrt{0.63} = 0.79")
Функция распределения F(X).
F(x<=0) = 0
F(0< x <=1) = 0.343
F(1< x <=2) = 0.441 + 0.343 = 0.784
F(2< x <=3) = 0.18900 + 0.784 = 0.973
F(x>3) = 1
- Вероятность появления события в одном испытании равна 0.6. Производится 5 испытаний. Составить закон распределения случайной величины Х – числа появлений события.
- Составить закон распределения случайной величины Х числа попаданий при четырех выстрелах, если вероятность попадания в цель при одном выстреле равна 0.8.
- Монету подбрасывают 7 раз. Найти математическое ожидание и дисперсию числа появлений герба. Примечание: здесь вероятность появление герба равна p = 1/2 (т.к. у монеты две стороны).
Пример №2. Вероятность появления события в отдельном испытании равна 0.6. Применяя теорему Бернулли, определите число независимых испытаний, начиная с которого вероятность отклонения частоты события от его вероятности по абсолютной величине меньше 0.1, больше 0.97. (Ответ: 801)
Пример №3. Студенты выполняют контрольную работу в классе информатики. Работа состоит из трех задач. Для получения хорошей оценки нужно найти правильные ответы не меньше чем на две задачи. К каждой задаче дается 5 ответов из которых только одна правильная. Студент выбирает ответ наугад. Какая вероятность того, что он получит хорошую оценку?
Решение. Вероятность правильно ответить на вопрос: p=1/5=0.2; n=3.
Эти данные необходимо ввести в калькулятор. В ответ см. для P(2)+P(3).
Пример №4. Вероятность попадания стрелка в мишень при одном выстреле равна (m+n)/(m+n+2). Производится n+4 выстрела. Найти вероятность того, что он промахнется не более двух раз.
Примечание. Вероятность того, что он промахнется не более двух раз включает в себя следующие события: ни разу не промахнется P(4), промахнется один раз P(3), промахнется два раза P(2).
Пример №5. Определите распределение вероятностей числа отказавших самолётов, если влетает 4 машины. Вероятность безотказной работы самолета Р=0.99. Число отказавших в каждом вылете самолётов распределено по биноминальному закону.
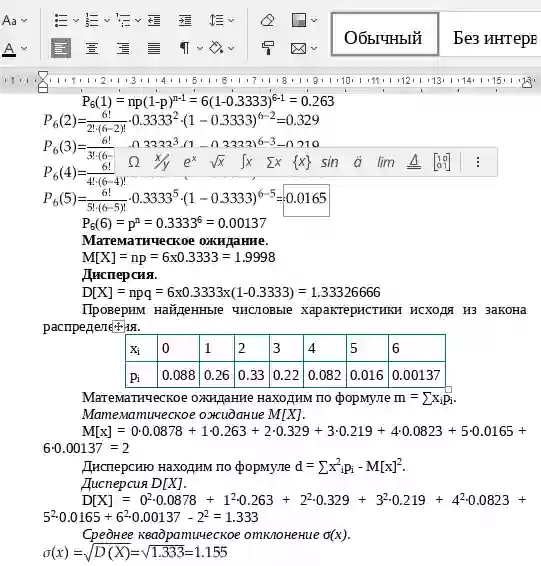
Задача 4. Среди 11 изделий 7 изделия первого сорта. Наудачу выбрали четыре изделия. случайная величина X – число первосортных изделий среди выбранных четырех изделий.
1. Составить закон распределения случайной величины X.
2. Построить полигон относительных частот.
3. Найти функцию распределения F(x) случайной величины X, построить ее график.
4. Найти характеристики случайной величины X:
а) математическое ожидание M(X);
б) дисперсию D(X), среднее квадратическое отклонение σ(Х);
в) моду M0.
Случайная величина X имеет область значений (0,1,2,...,n). Вероятности этих значений можно найти по формуле:
Pn(m) = Cmnpmqn-m
где Cmn - число сочетаний из n по m.
Найдем ряд распределения X.
P4(0) = (1-p)n = (1-0.636)4 = 0.0176
P4(1) = np(1-p)n-1 = 4(1-0.636)4-1 = 0.12
| xi | 0 | 1 | 2 | 3 | 4 |
| pi | 0,0176 | 0,12 | 0,32 | 0,37 | 0,16 |
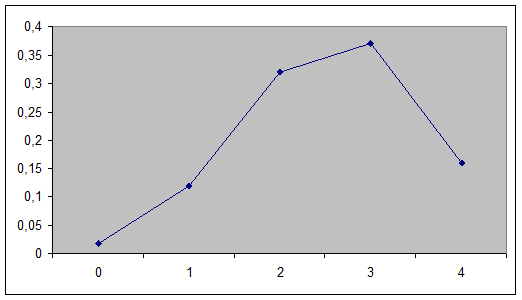
Мода равна тому значению X, при котором вероятность максимальная. В данном примере максимальная вероятность p =0,37 соответствует X = 3.
Математическое ожидание находим по формуле m = ∑xipi.
Математическое ожидание M[X].
M[x] = 0*0.0176 + 1*0.12 + 2*0.32 + 3*0.37 + 4*0.16 = 2.54
Дисперсию находим по формуле d = ∑x2ipi - M[x]2.
Дисперсия D[X].
D[X] = 02*0.0176 + 12*0.12 + 22*0.32 + 32*0.37 + 42*0.16 - 2.542 = 0.92601646
Среднее квадратическое отклонение σ(x).
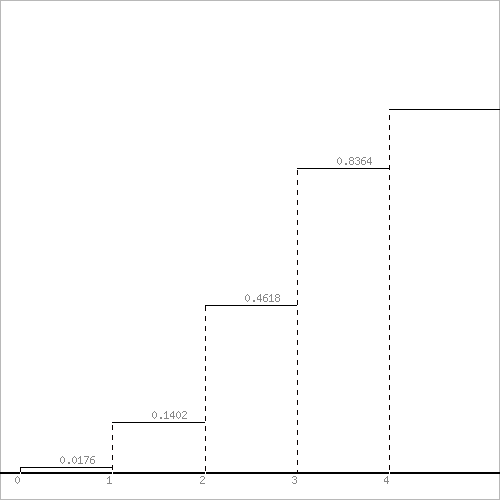
Функция распределения F(X).
F(x≤0) = 0
F(0< x ≤1) = 0.01755518
F(1< x ≤2) = 0.12269340 + 0.01755518 = 0.14024858
F(2< x ≤3) = 0.32156460 + 0.14024858 = 0.46181318
F(3< x ≤4) = 0.37456972 + 0.46181318 = 0.8363829
F(x>4) = 1
Пример 1. Вероятность того, что трамвай подойдет к остановке строго по расписанию, равна 0,7. X - число трамваев, прибывших по расписанию из 4 исследуемых. Составить закон распределения дискретной случайной величины X, вычислить M(X), D(X), σ(X), построить многоугольник распределения и график функции распределения F(X).
Решение. Случайная величина X имеет область значений (0,1,2,...,n). Вероятности этих значений можно найти по формуле:
Pn(m) = Cmnpmqn-m
где Cmn - число сочетаний из n по m.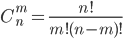
Найдем ряд распределения X.
P4(0) = (1-p)n = (1-0.7)4 = 0.0081
P4(1) = np(1-p)n-1 = 4(1-0.7)4-1 = 0.0756
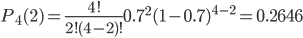
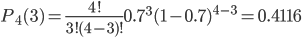
| x | 0 | 1 | 2 | 3 | 4 |
| p | 0.0081 | 0.0756 | 0.2646 | 0.4116 | 0.2401 |
Математическое ожидание M[X].
M[x] = 0*0.0081 + 1*0.0756 + 2*0.2646 + 3*0.4116 + 4*0.2401 = 2.8
Дисперсию находим по формуле d = ∑x2ipi - M[x]2.
Дисперсия D[X].
D[X] = 02*0.0081 + 12*0.0756 + 22*0.2646 + 32*0.4116 + 42*0.2401 - 2.82 = 0.84
Среднее квадратическое отклонение σ(x).
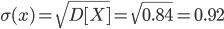
Пример 2. Вероятность того, что телевизор проработает гарантийный срок без поломки, равна 0.8. Закупили 4 телевизора. Какова вероятность того, что три телевизора не проработают гарантийный срок?
Решение. В поле вероятность вводим значение p = 1- 0 .8 = 0.2, поскольку нас интересует вероятность поломки.
