Биномиальное распределение
Биномиальное распределение симметрично только в его ограничивающей форме. Это распределение именуется так из-за его отношения к разложению двучлена (p + q)n. Биномиальное выражение – это выражение, которое содержит два члена, соединенных знаком «плюс» или «минус».Биномиальное распределение есть распределение вероятности исходов события, которые могут быть классифицированы как положительные или отрицательные, т.е. оно связано с обстоятельствами, в которых какое-либо специфическое событие может или случиться, или не случиться. Здесь нет места для полумер, и не принимается в расчет степень интенсивности события. Общая вероятность события, случающегося или не случающегося, равна 1. Поэтому если вероятность того, что оно случится, равна p, то вероятность того, что оно не случится, равна q = 1 – p, p + q = 1.
Члены p и q относятся к вероятности наступления или ненаступления только одного события. Вероятность наступления двух отдельных событий по закону умножения равна для независимых явлений: p × p = p2, т.е. 0,01 при p = 0,1. Вероятность ненаступления каждого из двух событий составляет q2 или 0,81. Но возникает новая серия возможностей, поскольку в первом случае возможность того, что событие случится, связана с тем, что оно не случится во втором случае; вероятность этого равна p × q или 0,09. Аналогичным образом вероятность наступления события во втором случае, связанная с ненаступлением в первом случае, также равна 0,09. Поэтому все вероятности в целом таковы:
· наступление события в обоих случаях – p2 = 0,01;
· ненаступление в обоих случаях – q2 = 0,81;
· наступление в первом и ненаступление во втором – pq = 0,09;
· наступление во втором и ненаступление в первом – qp = 0,09;
Общая вероятность всех исходов p2 + 2pq + q2 = 1,0.
Общая вероятность, таким образом, может быть алгебраически представлена как p2 + 2pq + q2 или (p + q)2. Соответственно там, где имеются три события, вероятности будут составлять:
· наступление события в трех случаях – p3 = 0,001;
· ненаступление события в трех случаях – q3 = 0,729;
· наступление в двух случаях и ненаступление в одном – 3p2q=0,027;
· наступление в одном случае и ненаступление в двух – 3pq2 = 0,243.
Общая вероятность всех исходов (p + q)3=1,0.
Подобным образом для n событий вероятности 0, 1, 2, 3, …, n того, что событие не произойдет, представлены соответственно последовательными членами разложения бинома (p + q)n. Общая вероятность всегда точно выражена единицей, поскольку (p + q) согласно определения равно 1, а из этого следует, что (p + q)n=1 каким бы не было значение n.
Там, где p=q=½, кривая биномиального распределения симметрична. Разложение (p + q)3, например, есть (p + q)3=p3 + 3p2q + 3pq2 + q3, и если p и q равны, то p3 и q3 тоже равны друг другу, а 3p2q=3pq2.
Там же, где p и q неравны, кривая не будет симметрична. Если, например, p=0,1 и q=0,9, кривая будет совершенно иной.
Построить биномиальное распределение можно с помощью калькулятора.
Числовые характеристики случайной величины
Графическое представление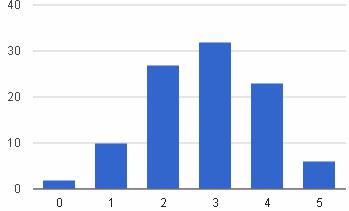
Плотность распределения биномиального распределения
pi = CNipiqN-i (схема Бернулли)
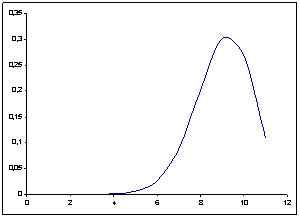
Математическое ожидание биномиального распределения
M[X] = np
Дисперсия биномиального распределения
D[X] = npq
Биномиальное, пуассоново и нормальное распределения являются главными из тех форм распределения, которыми пользуются для выполнения значительной части статистической работы.
Проверка ряда на соответствие биномиальному закону распределения.


