Математическое ожидание дискретной случайной величины
Математическим ожиданием (средним значением) случайной величины X, заданной на дискретном вероятностном пространстве, называется числоm=M[X]=∑xipi, если ряд сходится абсолютно.
Назначение сервиса. С помощью сервиса в онлайн режиме вычисляются математическое ожидание, дисперсия и среднеквадратическое отклонение (см. пример). Кроме этого строится график функции распределения F(X).
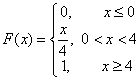 .
.
Свойства математического ожидания случайной величины
- Математическое ожидание постоянной величины равно ей самой: M[C]=C, C – постоянная;
- M[C•X]=C•M[X]
- Математическое ожидание суммы случайных величин равно сумме их математических ожиданий: M[X+Y]=M[X]+M[Y]
- Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: M[X•Y]=M[X]•M[Y], если X и Y независимы.
Свойства дисперсии
- Дисперсия постоянной величины равна нулю: D(c)=0.
- Постоянный множитель можно вынести из-под знака дисперсии, возведя его в квадрат: D(k*X)= k2D(X).
- Если случайные величины X и Y независимы, то дисперсия суммы равна сумме дисперсий: D(X+Y)=D(X)+D(Y).
- Если случайные величины X и Y зависимы: D(X+Y)=DX+DY+2(X-M[X])(Y-M[Y])
- Для дисперсии справедлива вычислительная формула:
D(X)=M(X2)-(M(X))2
Пример. Известны математические ожидания и дисперсии двух независимых случайных величин X и Y: M(x)=8, M(Y)=7, D(X)=9, D(Y)=6. Найти математическое ожидание и дисперсию случайное величины Z=9X-8Y+7.
Решение. Исходя из свойств математического ожидания: M(Z) = M(9X-8Y+7) = 9*M(X) - 8*M(Y) + M(7) = 9*8 - 8*7 + 7 = 23.
Исходя из свойств дисперсии: D(Z) = D(9X-8Y+7) = D(9X) + D(-8Y) + D(7) = 9^2D(X) + 8^2D(Y) + 0 = 81*9 + 64*6 = 1113
Алгоритм вычисления математического ожидания
Свойства дискретных случайных величин: все их значения можно перенумеровать натуральными числами; каждому значению сопоставить отличную от нуля вероятность.- Поочередно умножаем пары: xi на pi.
- Складываем произведение каждой пары xipi.
Например, для n = 4: m = ∑xipi = x1p1 + x2p2 + x3p3 + x4p4
Функция распределения дискретной случайной величины ступенчатая, она возрастает скачком в тех точках, вероятности которых положительны.
Пример №1.
| xi | 1 | 3 | 4 | 7 | 9 |
| pi | 0.1 | 0.2 | 0.1 | 0.3 | 0.3 |
Математическое ожидание находим по формуле m = ∑xipi.
Математическое ожидание M[X].
M[x] = 1*0.1 + 3*0.2 + 4*0.1 + 7*0.3 + 9*0.3 = 5.9
Дисперсию находим по формуле d = ∑x2ipi - M[x]2.
Дисперсия D[X].
D[X] = 12*0.1 + 32*0.2 + 42*0.1 + 72*0.3 + 92*0.3 - 5.92 = 7.69
Среднее квадратическое отклонение σ(x).
σ = sqrt(D[X]) = sqrt(7.69) = 2.78
Пример №2. Дискретная случайная величина имеет следующий ряд распределения:
| Х | -10 | -5 | 0 | 5 | 10 |
| р | а | 0,32 | 2a | 0,41 | 0,03 |
Решение. Величину a находим из соотношения: Σpi = 1
Σpi = a + 0,32 + 2a + 0,41 + 0,03 = 0,76 + 3a = 1
0.76 + 3a = 1 или 0.24=3a, откуда a = 0.08
Пример №3. Определить закон распределения дискретной случайной величины, если известна её дисперсия, причем х1<x2<x3<x4
x1=6; x2=9; x3=x; x4=15
p1=0,3; p2=0,3; p3=0,1; p4=0,3
d(x)=12,96
Решение.
Здесь надо составить формулу нахождения дисперсии d(x):
d(x) = x12p1+x22p2+x32p3+x42p4-m(x)2
где матожидание m(x)=x1p1+x2p2+x3p3+x4p4
Для наших данных
m(x)=6*0,3+9*0,3+x3*0,1+15*0,3=9+0.1x3
12,96 = 620,3+920,3+x320,1+1520,3-(9+0.1x3)2
или -9/100 (x2-20x+96)=0
Соответственно надо найти корни уравнения, причем их будет два.
x3=8, x3 =12
Выбираем тот, который удовлетворяет условию х1<x2<x3<x4
x3=12
Закон распределения дискретной случайной величины
x1=6; x2=9; x3=12; x4=15
p1=0,3; p2=0,3; p3=0,1; p4=0,3

