Формулы Бейеса
Формула Байеса: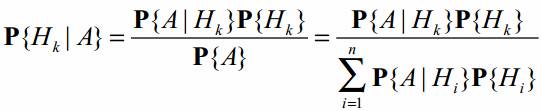
Вероятности P(Hi) гипотез Hi называют априорными вероятностями - вероятности до проведения опытов.
Вероятности P(A/Hi) называют апостериорными вероятностями – вероятности гипотез Hi, уточненных в результате опыта.
Пример №1. Прибор может собираться из высококачественных деталей и из деталей обычного качества. Около 40% приборов собираются из высококачественных деталей. Если прибор собран из высококачественных деталей, его надежность (вероятность безотказной работы) за время t равна 0,95; если из деталей обычного качества — его надежность равна 0,7. Прибор испытывался в течение времени t и работал безотказно. Найдите вероятность того, что он собран из высококачественных деталей.
Решение. Возможны две гипотезы: H1 — прибор собран из высококачественных деталей; H2 — прибор собран из деталей обычного качества. Вероятности этих гипотез до опыта: P(H1) = 0,4, P(H2) = 0,6. В результате опыта наблюдалось событие A — прибор безотказно работал время t. Условные вероятности этого события при гипотезах H1 и H2 равны: P(A|H1) = 0,95; P(A|H2) = 0,7. По формуле (12) находим вероятность гипотезы H1 после опыта:
Пример №2. Два стрелка независимо один от другого стреляют по одной мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка 0,8, для второго 0,4. После стрельбы в мишени обнаружена одна пробоина. Предполагая, что два стрелка не могут попасть в одну и ту же точку, найдите вероятность того, что в мишень попал первый стрелок.
Решение. Пусть событие A — после стрельбы в мишени обнаружена одна пробоина. До начала стрельбы возможны гипотезы:
H1 — ни первый, ни второй стрелок не попадет, вероятность этой гипотезы: P(H1) = 0,2 · 0,6 = 0,12.
H2 — оба стрелка попадут, P(H2) = 0,8 · 0,4 = 0,32.
H3 — первый стрелок попадет, а второй не попадет, P(H3) = 0,8 · 0,6 = 0,48.
H4 — первый стрелок не попадет, а второй попадет, P (H4) = 0,2 · 0,4 = 0,08.
Условные вероятности события A при этих гипотезах равны:
P(A|H1)=0; P(A|H2)=0; P(A|H3)=1; P(A|H4)=1.
После опыта гипотезы H1 и H2 становятся невозможными, а вероятности гипотез H3 и H4
будут равны:

Итак, вероятнее всего, что мишень поражена первым стрелком.
Пример №3. В монтажном цехе к устройству присоединяется электродвигатель. Электродвигатели поставляются тремя заводами-изготовителями. На складе имеются электродвигатели названных заводов соответственно в количестве 19,6 и 11 шт., которые могут безотказно работать до конца гарантийного срока соответственно с вероятностями 0,85, 0,76 и 0,71. Рабочий берет случайно один двигатель и монтирует его к устройству. Найдите вероятность того, что смонтированный и работающий безотказно до конца гарантийного срока электродвигатель поставлен соответственно первым, вторым или третьим заводом-изготовителем.
Решение. Первым испытанием является выбор электродвигателя, вторым — работа электродвигателя во время гарантийного срока. Рассмотрим следующие события:
A — электродвигатель работает безотказно до конца гарантийного срока;
H1 — монтер возьмет двигатель из продукции первого завода;
H2 — монтер возьмет двигатель из продукции второго завода;
H3 — монтер возьмет двигатель из продукции третьего завода.
Вероятность события A вычисляем по формуле полной вероятности:
P(A)=P(A|H1)·H1 + P(A|H2)·H2 + P(A|H3)·H3
Условные вероятности заданы в условии задачи:
P(A|H1)=0.85; P(A|H2)=0.76; P(A|H3)=0.71
Найдем вероятности P(H1)=19/36 ≈ 0,528; P(H2)=6/36 ≈ 0,167; P(H3)=11/36 ≈ 0,306;
P(A)=0,85·19/36+0,76·6/36+0,71·11/36 ≈ 0,792
По формулам Бейеса (12) вычисляем условные вероятности гипотез Hi:

Пример №4. Вероятности того, что во время работы системы, которая состоит из трех элементов, откажут элементы с номерами 1, 2 и 3, относятся как 3: 2: 5. Вероятности выявления отказов этих элементов равны соответственно 0,95; 0,9 и 0,6.
а) Найдите вероятность обнаружения отказа в работе системы.
б) В условиях данной задачи во время работы системы обнаружен отказ. Какой из элементов вероятнее всего отказал?
Решение.
Пусть А – событие отказа. Введем систему гипотез H1 – отказ первого элемента, H2 – отказ второго элемента, H3 – отказ третьего элемента.
Находим вероятности гипотез:
P(H1) = 3/(3+2+5) = 0.3
P(H2) = 2/(3+2+5) = 0.2
P(H3) = 5/(3+2+5) = 0.5
Согласно условию задачи условные вероятности события А равны:
P(A|H1) = 0.95, P(A|H2) = 0.9, P(A|H3) = 0.6
а) Найдите вероятность обнаружения отказа в работе системы.
P(A) = P(H1)*P(A|H1) + P(H2)*P(A|H2) + P(H3)*P(A|H3) = 0.3*0.95 + 0.2*0.9 + 0.5*0.6 = 0.765
б) В условиях данной задачи во время работы системы обнаружен отказ. Какой из элементов вероятнее всего отказал?
P1 = P(H1)*P(A|H1)/ P(A) = 0.3*0.95 / 0.765 = 0.373
P2 = P(H2)*P(A|H2)/ P(A) = 0.2*0.9 / 0.765 = 0.235
P3 = P(H3)*P(A|H3)/ P(A) = 0.5*0.6 / 0.765 = 0.392
Максимальная вероятность у третьего элемента.