Как решать задачи по теории вероятностей
- Задачи по теории вероятностей:
- сборник задач про шары в урне
- задачи на тему
Формула полной вероятности
На предприятии имеется три станка одного типа. Один из них дает 20% общей продукции, второй – 30%, третий – 50 %. При этом первый станок производит 5% брака, второй 4%, третий – 2%. Найти вероятность того, что случайно отобранное негодное изделие выпущено первым станком.
- Примеры задач по математической статистике.
- Вероятность попадания в интервал нормально распределенной случайной величины.
Заданы математическое ожидание а и среднее квадратическое отклонение s нормально распределённой случайной величины X. Требуется найти: а) вероятность того, что X примет значение, принадлежащее интервалу (a , b ); б) вероятность того, что абсолютная величина отклонения |X-а| окажется меньше d. - Как найти математическое ожидание непрерывной случайной величины:
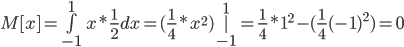
Построение полигона частот для СВ, эмпирические функции распределения.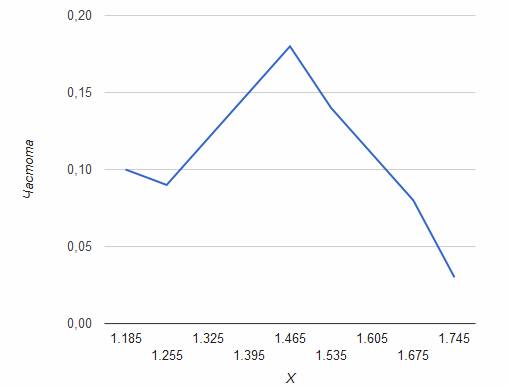
- Построить многоугольник распределения.
11,13,7,12,8,7,13,5,4,5 - Построение регрессионной модели по корреляционной таблице.
Системы случайных величин. Дискретная двумерная случайная величина (X,Y) задана матрицей распределения вероятностей. а) Зависимы ли случайные величины X и Y? б) Найдите условный закон распределения Y, если известно, что случайная величинаX=3.y/x 15 20 25 30 35 40 100 2 2 120 4 3 10 3 140 2 50 7 10 160 1 4 3 180 1 1
- Вероятность попадания в интервал нормально распределенной случайной величины.
- Примеры задач по статистике: показатели вариации, проверка гипотез о виде распределения, группировка статистических данных, доверительный интервал.
Составьте вариационный ряд по частотам или интервалам. Вычислить параметры распределения (среднюю выборочную, дисперсию, среднее квадратическое отклонение). Составить доверительный интервал X±2σ.
Статистические таблицы
- Распределение Стьюдента (t-распределение) для построения доверительного интервала.
- Распределение Фишера (F-распределение) для проверки значимости уравнения регрессии.
- Таблица значений функции Лапласа
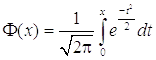
- Статистические таблицы Дарбина-Уотсона применяют, чтобы оценить автокорреляцию.
- Распределение ХИ квадрат (X
2 ). Используется для проверки гипотезы формы распределения ряда и определения доверительного интервала дисперсии.
Примеры решений по теории вероятностей и математической статистике
Задание. Вероятностный прогноз для величины Х -процентного изменения стоимости акций по отношению к их текущему курсу в течение 6 месяцев дан в виде закона распределения:| xi | 5 | 10 | 15 | 20 | 25 | 30 |
| pi | 0.1 | 0.1 | 0.3 | 0.2 | 0.2 | 0.1 |
Найти вероятность того, что покупка акций будет более выгодна, чем помещение денег на банковский депозит под 3% в месяц сроком на 6 месяцев.
Решение находим с помощью калькулятора.. Математическое ожидание находим по формуле m = ∑xipi.
Математическое ожидание M[X].
M[x] = 5*0.1 + 10*0.1 + 15*0.3 + 20*0.2 + 25*0.2 + 30*0.1 = 18
Дисперсию находим по формуле d = ∑x2ipi - M[x]2.
Дисперсия D[X].
D[X] = 52*0.1 + 102*0.1 + 152*0.3 + 202*0.2 + 252*0.2 + 302*0.1 - 182 = 51
Среднее квадратическое отклонение σ(x).
sigma(x) = sqrt{D[X]} = sqrt{51} = 7.14
Функция распределения F(X).
F(x<=5) = 0
F(5< x <=10) = 0.1
F(10< x <=15) = 0.1 + 0.1 = 0.2
F(15< x <=20) = 0.3 + 0.2 = 0.5
F(20< x <=25) = 0.2 + 0.5 = 0.7
F(25< x <=30) = 0.2 + 0.7 = 0.9
F(x>30) = 1
Вероятность.
P(a <= X <= b) = F(b) - F(a)
Пример №2. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х, заданной следующим законом распределения. Решение
Пример №3. Закон распределения дискретной случайной величины Х приведен в табл. Требуется: а) определить математическое ожидание М(X), дисперсию D(Х) и среднее квадратическое отклонение σ(Х) случайной величины Х; б) построить график этого распределения.
| xi | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| pi | 0.01 | 0.12 | 0.23 | 0.28 | 0.19 | 0.11 | 0.06 |
Математическое ожидание находим по формуле m = ∑xipi.
Математическое ожидание M[X].
M[x] = 0*0.01 + 1*0.12 + 2*0.23 + 3*0.28 + 4*0.19 + 5*0.11 + 6*0.06 = 3.09
Дисперсию находим по формуле d = ∑x2ipi - M[x]2.
Дисперсия D[X].
D[X] = 02*0.01 + 12*0.12 + 22*0.23 + 32*0.28 + 42*0.19 + 52*0.11 + 62*0.06 - 3.092 = 1.9619
Среднее квадратическое отклонение σ(x):
σ = sqrt(D[X]) = sqrt(1.96) = 1.4
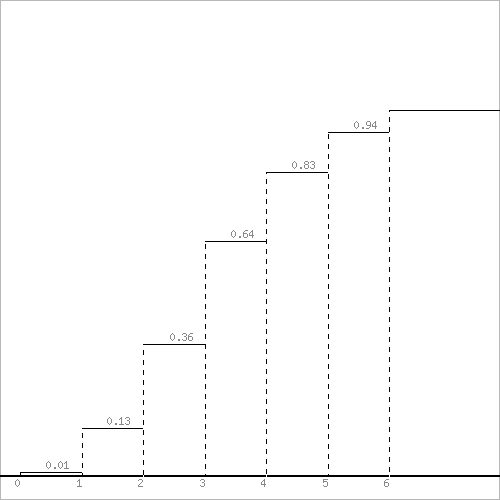
Функция распределения F(X).
F(x<=0) = 0
F(0< x <=1) = 0.01
F(1< x <=2) = 0.12 + 0.01 = 0.13
F(2< x <=3) = 0.23 + 0.13 = 0.36
F(3< x <=4) = 0.28 + 0.36 = 0.64
F(4< x <=5) = 0.19 + 0.64 = 0.83
F(5< x <=6) = 0.11 + 0.83 = 0.94
F(x>6) = 1
Функция распределения F(X)