Контрольная работа по теории вероятностей
Задание 1. Случайная величина Х задана функцией распределения F(x). Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины.Решение находим с помощью калькулятора. Случайная величина Х задана функцией распределения F(x):
0, x ≤ -1
(x+1)/2, -1<x<1
1, x ≥ 1
Найдем плотность распределения f(x), как производную от функции распределения F(x):
f(x) = dF(x)/dx = 1/2
Математическое ожидание.
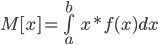
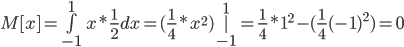
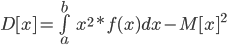
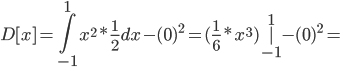
Среднеквадратическое отклонение.
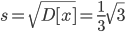
Задание 2. Расчетное задание включает предварительную обработку статистики, построение линейной регрессионной модели:
- Найти объем выборок, относительные частоты и накопленные относительные частоты. Если случайная величина (СВ) задана интервалами, то определить середины интервалов.
- Построить полигон частот, гистограмму для СВ.
- Найти эмпирическую функцию распределения, построить график.
- Определить числовые оценки параметров распределения.
Система случайных величин X и Y. Дискретная двумерная случайная величина (X,Y) считается заданной, если известен ее закон распределения: P(X=xi, Y=yj) = pij, i=1,2...,n, j=1,2..,m
| X / Y | 78 | 85 | 92 | 99 | 106 | 113 | 120 | 127 | 134 |
| 1.19 | 0 | 0 | 0 | 0 | 1 | 0 | 4 | 2 | 3 |
| 1.26 | 0 | 0 | 0 | 0 | 0 | 2 | 3 | 4 | 0 |
| 1.33 | 0 | 0 | 2 | 2 | 1 | 3 | 1 | 2 | 1 |
| 1.4 | 0 | 0 | 0 | 2 | 5 | 2 | 4 | 1 | 1 |
| 1.47 | 0 | 0 | 0 | 4 | 10 | 3 | 0 | 1 | 0 |
| 1.54 | 0 | 0 | 2 | 4 | 3 | 3 | 2 | 0 | 0 |
| 1.61 | 0 | 3 | 2 | 2 | 3 | 0 | 1 | 0 | 0 |
| 1.68 | 3 | 2 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 1.75 | 0 | 1 | 2 | 0 | 0 | 0 | 0 | 0 | 0 |
| X / Y | 78 | 85 | 92 | 99 | 106 | 113 | 120 | 127 | 134 |
| 1.19 | 0 | 0 | 0 | 0 | 0.01 | 0 | 0.04 | 0.02 | 0.03 |
| 1.26 | 0 | 0 | 0 | 0 | 0 | 0.02 | 0.03 | 0.04 | 0 |
| 1.33 | 0 | 0 | 0.02 | 0.02 | 0.01 | 0.03 | 0.01 | 0.02 | 0.01 |
| 1.4 | 0 | 0 | 0 | 0.02 | 0.05 | 0.02 | 0.04 | 0.01 | 0.01 |
| 1.47 | 0 | 0 | 0 | 0.04 | 0.1 | 0.03 | 0 | 0.01 | 0 |
| 1.54 | 0 | 0 | 0.02 | 0.04 | 0.03 | 0.03 | 0.02 | 0 | 0 |
| 1.61 | 0 | 0.03 | 0.02 | 0.02 | 0.03 | 0 | 0.01 | 0 | 0 |
| 1.68 | 0.03 | 0.02 | 0.01 | 0 | 0.01 | 0.01 | 0 | 0 | 0 |
| 1.75 | 0 | 0.01 | 0.02 | 0 | 0 | 0 | 0 | 0 | 0 |
1. Зависимость случайных величин X и Y.
Находим ряды распределения X и Y.
Пользуясь формулой ∑P(xi,yj) = pi (j=1..n), находим ряд распределения X.
| X | 1.19 | 1.26 | 1.33 | 1.4 | 1.47 | 1.54 | 1.61 | 1.68 | 1.75 | |
| P | 0.1 | 0.09 | 0.12 | 0.15 | 0.18 | 0.14 | 0.11 | 0.08 | 0.03 | ∑Pi = 1 |
M[x] = 1.185*0.1 + 1.255*0.09 + 1.325*0.12 + 1.395*0.15 + 1.465*0.18 + 1.535*0.14 + 1.605*0.11 + 1.675*0.08 + 1.745*0.03 = 1.44
Дисперсия D[X].
D[X] = 1.1852*0.1 + 1.2552*0.09 + 1.3252*0.12 + 1.3952*0.15 + 1.4652*0.18 + 1.5352*0.14 + 1.6052*0.11 + 1.6752*0.08 + 1.7452*0.03 - 1.442 = 0.0231
Среднее квадратическое отклонение σ(x).
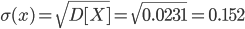
Пользуясь формулой ∑P(xi,yj) = qj (i=1..m), находим ряд распределения Y.
| Y | 78 | 85 | 92 | 99 | 106 | 113 | 120 | 127 | 134 | |
| P | 0.03 | 0.06 | 0.09 | 0.14 | 0.24 | 0.14 | 0.15 | 0.1 | 0.05 | ∑Pi = 1 |
M[y] = 78*0.03 + 85*0.06 + 92*0.09 + 99*0.14 + 106*0.24 + 113*0.14 + 120*0.15 + 127*0.1 + 134*0.05 = 108.24
Дисперсия D[Y].
D[Y] = 782*0.03 + 852*0.06 + 922*0.09 + 992*0.14 + 1062*0.24 + 1132*0.14 + 1202*0.15 + 1272*0.1 + 1342*0.05 - 108.242 = 189.02
Среднее квадратическое отклонение σ(y).
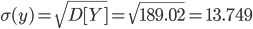
Поскольку, P(X=1.185,Y=78) = 0≠0.1•0.03, то случайные величины X и Y зависимы.
Полигон частот для СВ X
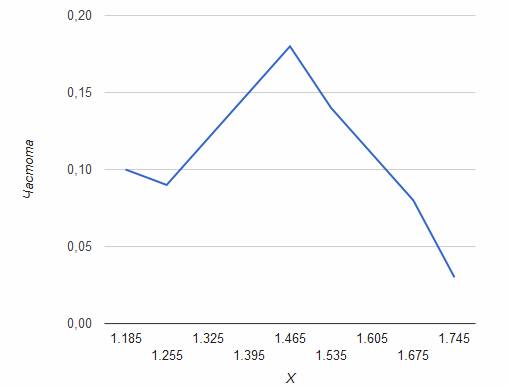
Полигон частот для СВ Y
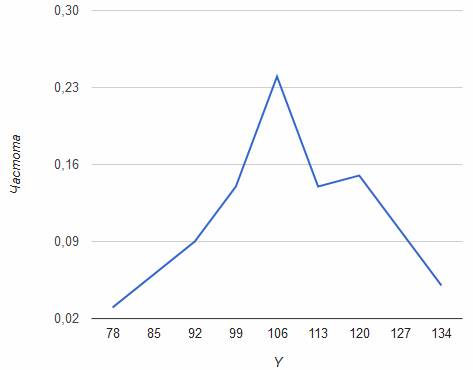

Полигон частот для СВ Y

Рассчитываем характеристики для СВ X.
| x | 1.185 | 1.255 | 1.325 | 1.395 | 1.465 | 1.535 | 1.605 | 1.675 | 1.745 |
| p | 0.1 | 0.09 | 0.12 | 0.15 | 0.18 | 0.14 | 0.11 | 0.08 | 0.03 |
Математическое ожидание M[X].
M[x] = 1.185*0.1 + 1.255*0.09 + 1.325*0.12 + 1.395*0.15 + 1.465*0.18 + 1.535*0.14 + 1.605*0.11 + 1.675*0.08 + 1.745*0.03 = 1.441
Дисперсию находим по формуле d = ∑x2ipi - M[x]2.
Дисперсия D[X].
D[X] = 1.1852*0.1 + 1.2552*0.09 + 1.3252*0.12 + 1.3952*0.15 + 1.4652*0.18 + 1.5352*0.14 + 1.6052*0.11 + 1.6752*0.08 + 1.7452*0.03 - 1.4412 = 0.0231
Среднее квадратическое отклонение σ(x).
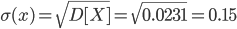
Функция распределения F(X).
F(x≤1.185) = 0
F(1.185< x ≤1.255) = 0.1
F(1.255< x ≤1.325) = 0.09 + 0.1 = 0.19
F(1.325< x ≤1.395) = 0.12 + 0.19 = 0.31
F(1.395< x ≤1.465) = 0.15 + 0.31 = 0.46
F(1.465< x ≤1.535) = 0.18 + 0.46 = 0.64
F(1.535< x ≤1.605) = 0.14 + 0.64 = 0.78
F(1.605< x ≤1.675) = 0.11 + 0.78 = 0.89
F(1.675< x ≤1.745) = 0.08 + 0.89 = 0.97
F(x>1.745) = 1
Рассчитываем характеристики для СВ Y.
| y | 78 | 85 | 92 | 99 | 106 | 113 | 120 | 127 | 134 |
| p | 0.03 | 0.06 | 0.09 | 0.14 | 0.24 | 0.14 | 0.15 | 0.1 | 0.05 |
Математическое ожидание M[y].
M[y] = 78*0.03 + 85*0.06 + 92*0.09 + 99*0.14 + 106*0.24 + 113*0.14 + 120*0.15 + 127*0.1 + 134*0.05 = 108.24
Дисперсию находим по формуле d = ∑y2ipi - M[y]2.
Дисперсия D[y].
D[y] = 782*0.03 + 852*0.06 + 922*0.09 + 992*0.14 + 1062*0.24 + 1132*0.14 + 1202*0.15 + 1272*0.1 + 1342*0.05 - 108.242 = 189.022
Среднее квадратическое отклонение σ(y).
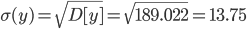
Функция распределения F(Y).
F(y≤78) = 0
F(78< y ≤85) = 0.03
F(85< y ≤92) = 0.06 + 0.03 = 0.09
F(92< y ≤99) = 0.09 + 0.09 = 0.18
F(99< y ≤106) = 0.14 + 0.18 = 0.32
F(106< y ≤113) = 0.24 + 0.32 = 0.56
F(113< y ≤120) = 0.14 + 0.56 = 0.7
F(120< y ≤127) = 0.15 + 0.7 = 0.85
F(127< y ≤134) = 0.1 + 0.85 = 0.95
F(y>134) = 1
