Задачи по теории вероятностей
см. также все возможные варианты задач про шары.Пример 1.
Наугад взяты два положительных числа, каждое из которых не превышает двух.
Решение:
a) Произведение не больше 1
A1 – взяли «1»![]() , A2 – затем снова взяли «1».
, A2 – затем снова взяли «1».
{1, 2}
![]() ;
; ![]()
P(A)=P(A1); ![]()
b) Отношение первого ко второму не больше двух
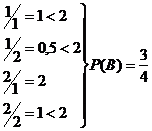
Пример 2.
Цифры 0 до 6. Сколько шестизначных черных чисел можно составить
Решение:
Формат: XXX XXX
Четные: 0, 2, 4, 6
![]()
Пример 3 (тема "Полная вероятность").
По самолету производят 4 независимых выстрела. Вероятность попадания 0,1. Чтобы вывести самолет из строя достаточно 3 попаданий.
P1=0,6 – выход самолета при одном попадании
P2=0,8 – выход самолета при двух попаданиях
P3=1 – выход самолета при трех попаданиях
Найти вероятность поражения самолета
Решение:
P(A1) – попали по самолету один раз (из 4-х)
P(A2) - попали по самолету два раза (из 4-х)
P(A3) - попали по самолету три раза (из 4-х)
P(A4) попали по самолету четыре раза (из 4-х)
P(A1)=C14·p1·q4-1; P(A2)=C24·p2·q4-2; P(A3)=C34·p3·q4-3; P(A4)=C44·p4·q4-4
Вероятность поражения
P=P(A1)·P1+P(A2)·P2+P(A3)·P3+P(A4)·P4 =
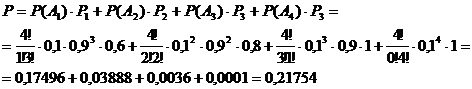
Пример 4.
I: 30%, высший сорт: 60%
II: 32%, высший сорт: 25%
III:38%, высший сорт: 50%
Найти вероятность того, что из 300 изделий, взятых наугад, число изделий высшего сорта заключено между 130 и 170.
Решение:
A – высший сорт, Bi – с i-ого завода, Ci – высший сорт
P(A)=ΣP(Bi) P(Ci)
P(A)=P(B1) P(C1)+ P(B2) P(C2)+P(B3) P(C3)=0,3·0,6+0,32·0,25+0,38·0,5=0,45, p=0,45, q=0,55
Наивероятнейшее число:
n·p-q<k< n·p+p, 300·0,45-0,55<k<300·0,45+0,55
135,5<k<135,45, k=135
170-135=35, 170-130=40
![]()
I автомат – 20%, 0,2% - брака
II автомат – 30%, 0,3% - брака
III автомат – 50%, 0,1% - брака
Найти вероятность того, что поступившая на сборку деталь – бракованная.
![]() - вероятность того, что деталь с I автомата
- вероятность того, что деталь с I автомата
![]() - с II станка,
- с II станка,
![]() - с III станка
- с III станка
![]() - вероятность брака с I автомата
- вероятность брака с I автомата
![]() - вероятность брака с II автомата
- вероятность брака с II автомата
![]() - вероятность брака с III автомата
- вероятность брака с III автомата
P=PI·PIб+PII·PIIб+PIII·PIIIб = 0,2·0,002+0,3·0,003+0,5·0,001=0,0018
Пример 10.
Задание: Охотник выстрелил 3 раза по удаляющейся цели. Вероятность попадания в нее в начале стрельбы 0,8, а после каждого выстрела уменьшается на 0,1. Найти вероятность того, что охотник попал в цель хотя бы 1 раз.
Решение:
Произведено 3 выстрела
P1=0,8; P2=0,7; P3=0,6
P(A) – вероятность того, что охотник попал в цель хотя бы 1 раз
P(Ā) – охотник не попал ни разу
P(Ā)=P(B1)·P(B2)·P(B3)=0,2·0,3·0,4=0,024
P(A)=1- P(Ā)=1-0,024=0,976
Пример 11.
Задание: Вероятность одного попадания в цель при одном залпе из 2-х орудий равна 0,38. Найти вероятность поражения цели при одном выстреле первым из орудий, если для второго орудия эта вероятность 0,8.
Решение:
P(A)=0,38 – вероятность попадания в цель при одном залпе из 2-х орудий
P(B2)=0,8 – вероятность поражения цели вторым орудием
P(A1) – поразили цель из 1-ого орудия
P(A)=P(A1)·P(B2)·P(B1) P(A2)
B2 – не попали из 2-го оружия
A1 – из второго орудия поразили цель
P(A2)=1- P(B2)
0,38=P(A1)·0,2+[1-P(A1)]·0,8
0,38=0,2·P(A1)+ 0,8-0,8P(A1)
-0,42=-0,6P(A1); P(A1)=0,7
Вероятность того, что первым попал снаряд из 1-го орудия P=0,7
Пример 12.
В магазин вошли n покупателей. Найти вероятность того, что m из них совершит покупку (P=0,1 – вероятность того, что кто-то купит)
n=11, m=7, p=0,1, q=0,9
Pn(m)=Cmn·pm·qn-m
Пример 13.
Брак 5%. Составить закон распределения числа брак. изделий из трех взятых наугад.
![]() ,
, ![]() , n=3
, n=3
Pn(m)=Cmn·pm·qn-m
| X | 0 | 1 | 2 | 3 |
| P | 0,8574 | 0,1354 | 0,0071 | 0,000125 |
Пример 14.
Партия 100 деталей, из которых 10 бракованные. Выбраны случайным образом 5 для проверки качества. Выстроить закон распределения числа бракованных изделий, содержащихся в выборке.
Решение:
N=100, n=10 – брак, ![]() - вероятность брака
- вероятность брака
![]() - деталь не бракованная
- деталь не бракованная
Всего возможны 6 вариантов:
1) нет бракованных
2) 1 бракованная
3) 2 бракованных
4) 3 бракованных
5) 4 бракованных
6) Все 5 бракованные
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | 0,59 | 0,33 | 0,073 | 0,0081 | 0,00045 | 0,00001 |
Пример 15.
Из 100 билетов 2 выигрышные: 210 и 60 руб.
Составить закон распределения суммы выигрыша для лица, имеющего 2 билета
Решение:
P0 – вероятность того, что ничего не выиграли
![]()
P1 – вероятность выигрыша одного билета.
P2 – вероятность выигрыша сразу 2-х билетов
| X | 0 | 60 | 210 | 270 |
| P | 0,9801 | 0,0099 | 0,0099 | 0,0001 |
M(x)=∑Pi·Xi = 0·0,9801 + 60·0,0099 + 210·0,0099 + 270·0,0001 = 2,7
D(x)=M(x2)-[M(x)]2=ΣPiXi2-[M(x)]2
D(x) = 02·0,9801 + 602·0,0099 + 2102·0,0099 + 2702·0,0001 - 2,72 = 472,23
Пример 16.
F(x)=4·e-4x
Мода: max(f(x))
Max(4·e-4x): нет max, нет моды
Медиана: P(x<me)= P(x>me), P(0<x< me)=½
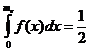 ;
;
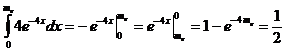
Me=0,173
Вероятность попадания в интервал
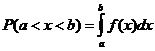
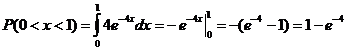
Пример 17.
Сколько раз надо бросить монету, чтобы с вероятностью 0,6 можно было ожидать, что отклонение относительной частоты появления герба от вероятности 0,5 окажется по абсолютной величине не более 0,01
Решение:
ε=0,01; p=0,6; q=0,4
![]()
![]()
![]()
![]()
По таблице φ(0,84)=0,3; ![]()
![]() , n=17,64≈18
, n=17,64≈18
Пример 18.
P=0,1 – вероятность наугад взятой детали
Сколько нужно взять деталей, чтобы наивероятнейшее число годных было 50.
Решение:
Q=0,1 – брак, p=0,9 – годная
n·p-q≤k0≤n·p+p
n·0,9-0,1≤50≤n·0,9+0,9
n<55,67
n>54,56
n=55
Пример 19.
Диаметр детали – случайная величина, распределенная по нормальному закону.
D(x)=0,0004 см.2, M(x)=3,7 см., P=0,9973
В каких границах можно гарантировать диаметр детали.
Решение:
P(|x-mx|<σt)=2φ(t)
![]()
По таблице x=3
![]()
Интервал: (mx-x·σ;mx+x·σ)
(3,7-3·0,02; 3,7+3·0,02)=(3,64; 3,88)
Ответ: (3,64; 3,88)
Пример 21.
20% деталей удовлетворяют определенным требованиям. Наугад берется 5 деталей. Число рассматриваемых – случайная величина.
Решение:
1) Распределение вероятностей
![]() - удовлетворяют требованиям
- удовлетворяют требованиям
![]() - не удовлетворяют требованиям
- не удовлетворяют требованиям
Pn(K)=Cnk·pk·qn-k
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | 0,32768 | 0,4096 | 0,2048 | 0,0512 | 0,0064 | 0,00032 |
2) График полигона.
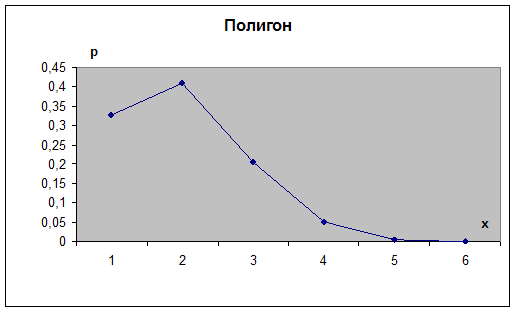
3)Математическое ожидание
M(x)=Σpi·xi
M(x)=0·0,32768+1·0,4096+2·0,2048+3·0,0512+4·0,0064+5·0,00032=1
4) D(x)=M(x2)-[M(x)]2
D(x)= 02·0,32768+12·0,4096+22·0,2048+32·0,0512+42·0,0064+52·0,00032=12=1,8-1=0,8
5) Наивероятнейшее число
n·p-q≤k0<n·p+p
n=5, p=1/5, q=4/5
