Формула полной вероятности
Если события H1, H2, …, Hn образуют полную группу, то для вычисления вероятности произвольного события можно использовать формулу полной вероятности:Из формулы полной вероятности следует формула Байеса:
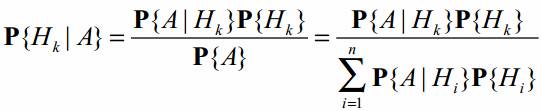
Вероятности P(Hi) гипотез Hi называют априорными вероятностями - вероятности до проведения опытов.
Вероятности P(A/Hi) называют апостериорными вероятностями – вероятности гипотез Hi, уточненных в результате опыта.
Назначение сервиса. Онлайн-калькулятор предназначен для вычисления полной вероятности с оформлением всего хода решения в формате Word (см. примеры решения задач).
Пример №1. Магазин получает электролампочки с двух заводов, причем доля первого завода составляет 25%. Известно, что доля брака на этих заводах равна соответственно 5 % и 10 % от всей выпускаемой продукции. Продавец наугад берет одну лампочку. Какова вероятность того, что она окажется бракованной?
Решение: Обозначим через А событие - «лампочка окажется бракованной». Возможны следующие гипотезы о происхождении этой лампочки: H1 - «лампочка поступила с первого завода». H2- «лампочка поступила со второгозавода». Так как доля первого завода составляет 25 %, то вероятности этих гипотез равны соответственно 
; 
.
Условная вероятность того, что бракованная лампочка выпущена первым заводом – 
, вторым заводом - p(A/H2)=
искомую вероятность того, что продавец взял бракованную лампочку, находим по формуле полной вероятности
р(А) = P(H1)· p(A/H1)+P(H2)·(A/H2)=0,25·0,05+0,75·0,10=0,0125+0,075=0.0875
Ответ: р(А) = 0,0875.
Построение гипергеометрического распределения.
Пример №2. Магазин получил две равные по количеству партии одноименного товара. Известно что, 25% первой партии и 40% второй партии составляет товар первого сорта. Какова вероятность того, что наугад выбранная единица товара будет не первого сорта?
Решение:
Обозначим через А событие - «товар окажется первого сорта». Возможны следующие гипотезы о происхождении этого товара: H1 - «товар из первой партии». H2- «товар из второй партии». Так как доля первой партии составляет 25%, то вероятности этих гипотез равны соответственно ; 
.
Условная вероятность того, что товар из первой партии – 
, из второй партии - 
искомую вероятностьтого, что наугад выбранная единица товара будет первого сорта
р(А) = P(H1)· p(A/H1)+P(H2)·(A/H2)=0,25·0,5+0,4·0,5=0,125+0,2=0.325
Тогда, вероятность того, что наугад выбранная единица товара будет не первого сорта будет равна: 1- 0.325 = 0,675
Ответ: 
.
Пример №3. Известно, что 5% мужчин и 1% женщин - дальтоники. Наугад выбранный человек оказалась не дальтоником. Какова вероятность, что это мужчина (считать, что мужчины и женщины поровну).
Решение.
Событие A - наугад выбранный человек оказалась не дальтоником.
Найдем вероятность появления этого события.
P(A) = P(A|H=мужчина) + P(A|H=женщина) = 0.95*0.5 + 0.99*0.5 = 0.475 + 0.495 = 0.97
Тогда вероятность, что это мужчина составит: p = P(A|H=мужчина) / P(A) = 0.475/0.97 = 0.4897
Пример №4. В спортивной олимпиаде принимают участие 4 студента с первого курса, с второго - 6, с третьей - 5. Вероятности того, что студент с первого, второго, третьего курса победит на олимпиаде, равны соответственно 0,9; 0,7 и 0,8.
а) Найдите вероятность победы наугад выбранным ее участником.
б) В условиях данной задачи один студент победил на олимпиаде. К какой группе он вероятнее всего принадлежит?
Решение.
Событие A - победа наугад выбранного участника.
Здесь P(H1) = 4/(4+6+5) = 0.267, P(H2) = 6/(4+6+5) = 0.4, P(H3) = 5/(4+6+5) = 0.333,
P(A|H1) = 0.9, P(A|H2) = 0.7,P(A|H3) = 0.8
а) P(A) = P(H1)*P(A|H1) + P(H2)*P(A|H2) + P(H3)*P(A|H3) = 0.267*0.9 + 0.4*0.7 + 0.333*0.8 = 0.787
б) Решение можно получить, используя этот калькулятор.
p1 = P(H1)*P(A|H1)/P(A)
p2 = P(H2)*P(A|H2)/P(A)
p3 = P(H3)*P(A|H3)/P(A)
Из p1, p2, p3 выбрать максимальную.
Пример №5. На предприятии имеется три станка одного типа. Один из них дает 20% общей продукции, второй – 30%, третий – 50 %. При этом первый станок производит 5% брака, второй 4%, третий – 2%. Найти вероятность того, что случайно отобранное негодное изделие выпущено первым станком.
